Question

The area of the region bounded by $y=3x+1,y=2x+1$and $x=4$ is \[\]
A. $16$ sq. unit \[\]
B. $\dfrac{121}{3}$ sq. unit \[\]
C. $\dfrac{121}{6}$ sq. unit\[\]
D. $8$ sq. unit\[\]

Answer 1

Hint: We plot given lines $y=3x+1,y=2x+1$ by joining the points of intersection with the axes. We see both the lies intercept $y-$axis at $A\left( 0,1 \right)$. We plot the third line $x=4$ and finds its point of intersection with $y=3x+1$at $E\left( 4,13 \right)$ and with $y=2x+1$ at $F\left( 4,9 \right)$. The area enclosed by the three lines is area of the triangle AEF. \[\]

Complete step by step answer:
We know that points of intersection are the points of intersection of line with coordinate axes. If the equation of line is $ax+by+c=0$ then we put $x=0$ to find the point of intersection with $y$ axis as $\left( 0,\dfrac{-c}{b} \right)$ and we put $y=0$ to find point of intersection as $\left( \dfrac{-c}{a},0 \right)$.
We are given in the question equations of three lines.
\[\begin{align}
  & y=3x+1......\left( 1 \right) \\
 & y=2x+1........\left( 2 \right) \\
 & x=4.....\left( 3 \right) \\
\end{align}\]
We put $x=0$ and then $y=0$ in equation of line (1) and get the coordinates of points of intersection with the axes $\left( 0,1 \right),\left( 0,\dfrac{-1}{3} \right)$.We plot line (1) by joining points of intersection of denoted as $A\left( 0,1 \right),B\left( 0,\dfrac{-1}{3} \right)$. \[\]
We put $x=0$ and then $y=0$ in equation of line (2) and get the coordinates of points of intersection with the axes$\left( 0,1 \right),\left( 0,\dfrac{-1}{2} \right)$. We plot line (2) by joining its points of intersection denoted as $A\left( 0,1 \right),C\left( 0,\dfrac{-1}{2} \right)$. \[\]
We draw line (3) as parallel to the $y-$axis and perpendicular to $x-$axis at the point $D\left( 4,0 \right)$. We put $x=4$ in equation of line (1) and find the point of intersection with line (3) and (1) as $E\left( 4,13 \right)$. We put $x=4$ in equation of line (2) and find the point of intersection with line (3) and (2) as $F\left( 4,9 \right)$. The rough figure is given below. \[\]

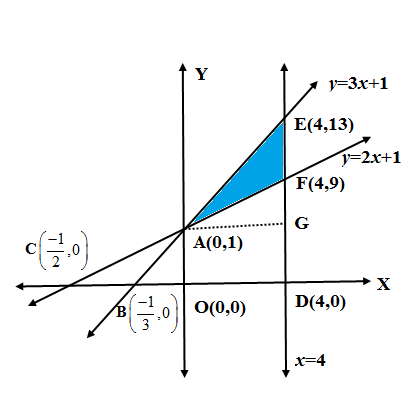
The area enclosed by the lines $y=3x+1,y=2x+1,x=4$ is the area of the triangle AEF. We take EF as the base of the triangle and drop altitude AG on the line containing EF. So we have from the construction $AG=OD$. We use the distance formula for distance between two points to find EF and AG. We have
\[\begin{align}
  & EF=\sqrt{{{\left( 4-4 \right)}^{2}}+{{\left( 13-5 \right)}^{2}}}=\sqrt{{{4}^{2}}}=4 \\
 & AG=OD=\sqrt{{{\left( 4-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=\sqrt{{{4}^{2}}}=4 \\
\end{align}\]
So the area of the triangle is
\[\text{Area}=\dfrac{1}{2}\times EF\times AG=\dfrac{1}{2}\times 4\times 4=8\text{ sq}\text{. unit}\]

So, the correct answer is “Option D”.

Note: e note that distance (which is always positive) between any two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ in plane is given by $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$. We can find the area of the area of triangle ABC as difference in areas of trapezium OAED and OAFD. We can also find the area enclosed using definite integral by taking the difference of area under the curve $y=3x+1$ and $y=2x+1$within the limits $x=0$ to $x=4$.