Question

The area of the trapezium is 1586 sq. m. The length of its parallel sides are 38 cm and 84 cm. Find the distance between them.

Answer 1

Hint: Here, we will draw the diagram using the given information. We will substitute the given values in the formula of area of trapezium. Then we will simplify it to find the distance between the parallel sides by using the area of the trapezium formula. Area of the trapezium is defined as the region covered by the trapezium.

Formula Used:
We will use the formula Area of the Trapezium \[ = \dfrac{1}{2} \times \left( {a + b} \right) \times h\] , where \[a\] and \[b\] are the parallel sides and \[h\] is the perpendicular distance between the parallel sides.

Complete step-by-step answer:
First we will draw the diagram of the trapezium based on the given information.

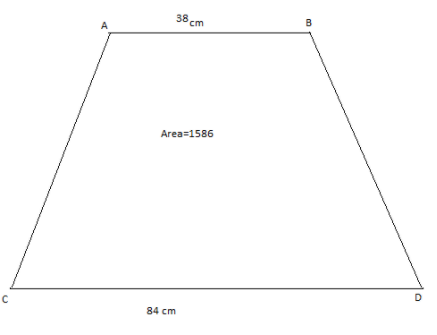
We will substitute the length of the parallel sides and in the formula for area of trapezium.
Substituting \[a = 38\], \[b = 84\] and \[A = 1586\] in the formula Area of the Trapezium \[ = \dfrac{1}{2} \times \left( {a + b} \right) \times h\], we get
\[ \Rightarrow 1586 = \dfrac{1}{2} \times \left( {38 + 84} \right) \times h\]
Adding the terms, we get
\[ \Rightarrow 1586 = \dfrac{1}{2} \times 122 \times h\]
Dividing 122 by 2, we get
\[ \Rightarrow 1586 = 61 \times h\]
Again dividing 1586 by 61, we get
\[ \Rightarrow h = \dfrac{{1586}}{{61}}\]
\[ \Rightarrow h = 26{\rm{cm}}\]
Therefore, the distance between the parallel sides is 26cm.

Note: We know that the trapezium is also known as trapezoid. A trapezium has two parallel sides and two non-parallel sides. The diagonals of a trapezium bisect each other. The length of the mid-segment is equal to half of the sum of the bases of parallel sides, in a trapezium. Trapezium has a wide number of applications. For example, Roof of a building is in the form of trapezium. If the perpendicular distance between them and the length of the parallel sides are known, then we can find the area of the trapezium.