Question

The area under the acceleration-time graph gives:
A.) Distance travelled
B.) Change in direction
C.) Force acting
D.) Change in velocity

Answer 1

Hint: Try to understand the concept of graphs between two physical quantities. Draw an acceleration-time graph. Try to find the area of the graph with the help of physical notations. Then we can find our answer.

Complete step by step answer:
An acceleration-time graph is represented as the acceleration on the y-axis or the vertical axis and time in the x-axis or the horizontal axis. The value of the graph at a particular time will give us the acceleration of the object at that point of time.

Slope of an acceleration-time graph is known as a jerk. It gives us the rate of change of acceleration.

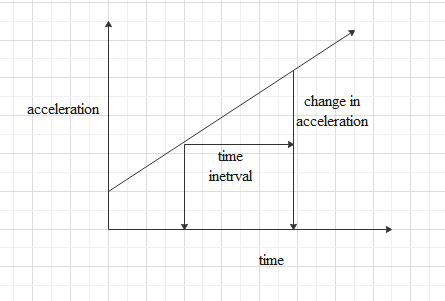
We can find the area under the acceleration-time graph for a certain time interval.

Area under the graph can be defined as, $\text{area }=\Delta a\times \Delta t$

Where, $\Delta t$ is the time interval and $\Delta a$ the change in acceleration in that time interval.

Now we can find acceleration as,

$\Delta a=\dfrac{\Delta v}{\Delta t}$

So, by multiplying both sides of equation by $\Delta t$ , we can write,

$\Delta a\times \Delta t=\Delta v$

So, the area under the acceleration-time graph can be given as,

$\text{area }=\Delta a\times \Delta t=\Delta v$

Which is the rate of change of velocity.

So, the area under any acceleration time graph at a certain time interval will give us the rate of change of velocity.

The correct option is (a).

Note: For a constant acceleration we will get a linear graph parallel to the time axis. If we have a uniformly increasing acceleration, we will get a straight line with a slope. For non-uniform acceleration we won’t get a straight-line graph.