Question

The area under the force-displacement curve represents.
A. velocity
B. Acceleration
C. Impulse
D. work is done

Answer 1

Hint: We know that integrating a curve in an x-y plane within the prescribed limits of x can give us the area under that curve. An integration can sum up the small area elements over the given limits to provide the final resultant area.

Complete step by step answer:
 The force acting on the system is constant, for example, when a force of gravity and friction moves with the constant speed, therefore the force-displacement graph is just a horizontal line because force can’t change.

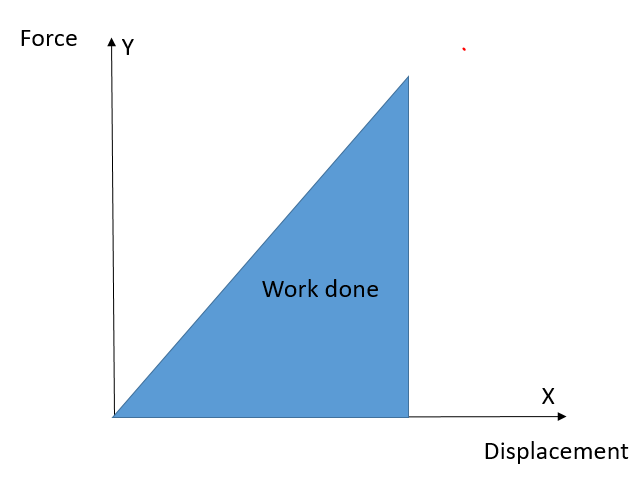
In this case, the area under the graph is triangular, with base length (S) that is displacement height (H). So, the area of the triangle is 0.5×base×height.
Now here in the above figure, the area under the line that is blue represents the work done by force.
Since we can say that force is a function of x, let’s say F(x) then the work is given by,

Here W is the work done, and dx is the differential distance, and when we integrate the sum of F(x)dx continually with integration, then we will get the required work done. Here 0 to x is the range of displacement within which the work is calculated.
 From this formula, we calculate the mechanical work done by a constant force.
We can also use this method to calculate the work done when an object accelerates from rest to final speed (v), using a constant force F. For a constant acceleration from rest, the distance travelled can be written in terms of the average rate (V_av)
$\therefore {\rm{S = }}{{\rm{V}}_{{\rm{av}}}} \times {\rm{t = }}\dfrac{{{\rm{Vt}}}}{2}$
And the acceleration (a) becomes,
${\rm{a = }}\dfrac{{\rm{v}}}{{\rm{t}}}$ (Here v is velocity and t is time.)
So, the work is done, ${\rm{W = F}}{\rm{.S}}$
$ \Rightarrow {\rm{W = m}} \times {\rm{a}} \times {\rm{S = m}} \times \dfrac{{\rm{v}}}{{\rm{t}}} \times \dfrac{{{\rm{vt}}}}{2} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}$
So the work is done, when objects accelerate to a constant speed from rest is equal to the energy stored as kinetic energy by the conservation of energy.

Note: When we talk about the graph of force-displacement, it means the force is a function of some displacement. Therefore the nature of the graph and its slope will depend upon the nature of the function. No work is done along the direction of the motion if the force is perpendicular.