
The areas of three adjacent faces of a rectangular box which meet in a point are known. The product of these areas is equal to
A. the volume of the box
B. twice the volume of the box
C. the square of the volume of the box
D. the cube root of the volume of the box
Answer
479.4k+ views
Hint: We denote the denote the vertices of the cuboid shaped rectangular box as A, B, C, D, E, F, G, H and three different sides length, breadth and height denoted
Complete step by step answer:
We know that a cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted
The amount of space contained by a three dimensional object is measured by the quantity called volume. The amount of space that is occupied by a cuboid is the product of length, breadth and height. Mathematically, volume denoted as
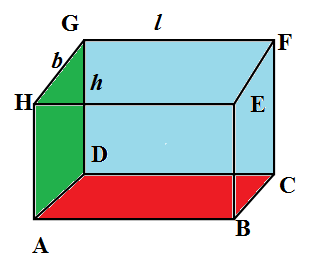
Let us denote the vertices of the cuboid as A, B, C, D, E, F, G, H. We are going to call two rectangular surfaces adjacent when they share a common vertex. We have the rectangular surfaces ABCD, DCFG and ADGH share the common vertex D. Let us assign
We are given the question that the areas of three adjacent faces of a rectangular box which meet in a point are known. The rectangular face is the product of its different sides. So the areas of three adjacent faces are
So the product surface areas of the three adjacent faces is
.We use value for equation (1) and have;
The product of these areas is equal to the square of the volume.
So, the correct answer is “Option C”.
Note: A cube is cuboid with all sides of equal length which means
Complete step by step answer:
We know that a cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted
The amount of space contained by a three dimensional object is measured by the quantity called volume. The amount of space that is occupied by a cuboid is the product of length, breadth and height. Mathematically, volume denoted as

Let us denote the vertices of the cuboid as A, B, C, D, E, F, G, H. We are going to call two rectangular surfaces adjacent when they share a common vertex. We have the rectangular surfaces ABCD, DCFG and ADGH share the common vertex D. Let us assign
We are given the question that the areas of three adjacent faces of a rectangular box which meet in a point are known. The rectangular face is the product of its different sides. So the areas of three adjacent faces are
So the product surface areas of the three adjacent faces is
.We use value for equation (1) and have;
The product of these areas is equal to the square of the volume.
So, the correct answer is “Option C”.
Note: A cube is cuboid with all sides of equal length which means
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




