The axis of a parabola is y=x, and the vertex and the focus are at a distance $\sqrt 2 $ and $2\sqrt 2 $ respectively from the origin, Then, equation of the parabola is
$
(a){\text{ (x - y}}{{\text{)}}^2} = 8(x + y - 2) \\
(b){\text{ (x + y}}{{\text{)}}^2} = 2(x + y - 2) \\
(c){\text{ (x - y}}{{\text{)}}^2} = 4(x + y - 2) \\
(d){\text{ (x + y}}{{\text{)}}^2} = 2(x - y + 2) \\
$
Answer
Verified498.3k+ views
Hint – In this question consider the vertex of the parabola as (c, d) and the coordinates of focus of the parabola as (e, f). Use the distance formula that is $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $for any two pairs of point$({x_1},{y_1}){\text{ and (}}{{\text{x}}_2},{y_2})$, to get the value of c, d, e and f. Then use them to find the equation of parabola.
Complete step-by-step answer:
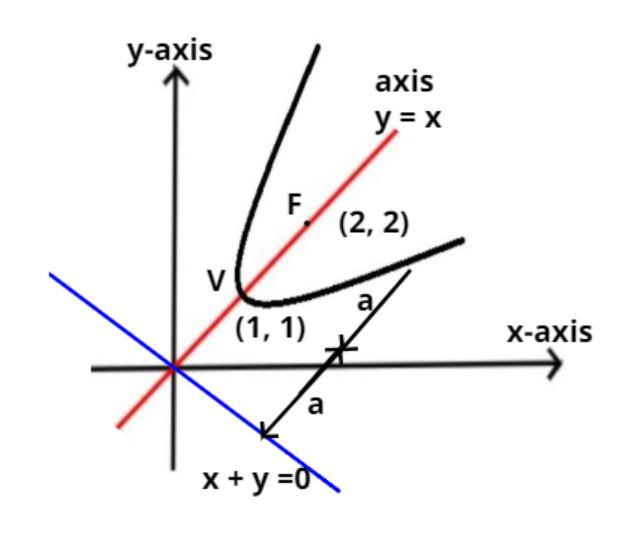
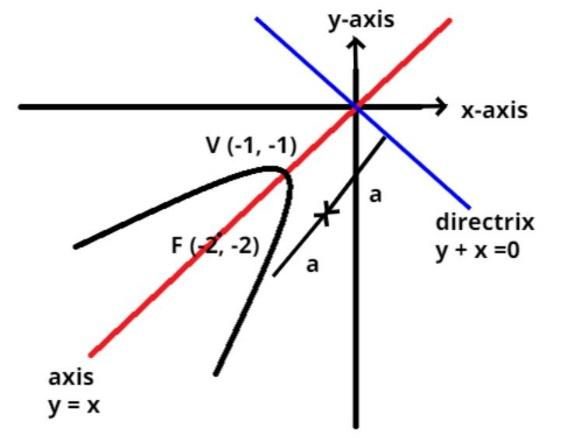
It is given that the axis of the parabola is y = x.
And the vertex of the parabola is $\sqrt 2 $ from the origin.
Let the coordinates of the vertex of the parabola be (c, d).
The distance between any two pair of points $({x_1},{y_1}){\text{ and (}}{{\text{x}}_2},{y_2}){\text{ is }}\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
So the distance between origin (0, 0) and (c, d) is $\sqrt 2 $
$ \Rightarrow \sqrt 2 = \sqrt {{{\left( {d - 0} \right)}^2} + {{\left( {c - 0} \right)}^2}} $
Now squaring on both sides we have,
$ \Rightarrow 2 = {\left( d \right)^2} + {\left( c \right)^2}$
It is given that the axis of the parabola is y = x, as the vertex lies on the axis therefore, c = d.
$ \Rightarrow {c^2} + {c^2} = 2$
$ \Rightarrow 2{c^2} = 2$
$ \Rightarrow {c^2} = 1$
Now take square root we have,
$ \Rightarrow c = \pm 1$
$ \Rightarrow c = d = \pm 1$
So the vertex of the parabola is (1, 1) or (-1, -1)
Now it is also given that the distance of the focus of the parabola from the origin is$2\sqrt 2 $.
Let the coordinates of the focus of the parabola be (e, f).
So the distance between origin (0, 0) and (e, f) is $2\sqrt 2 $
$ \Rightarrow 2\sqrt 2 = \sqrt {{{\left( {f - 0} \right)}^2} + {{\left( {e - 0} \right)}^2}} $
Now squaring on both sides we have,
$ \Rightarrow {\left( {2\sqrt 2 } \right)^2} = {\left( e \right)^2} + {\left( f \right)^2}$
$ \Rightarrow {e^2} + {f^2} = 8$
It is given that the axis of the parabola is y = x, as the vertex is also lying on the axis therefore, e = f
$ \Rightarrow {e^2} + {e^2} = 8$
$ \Rightarrow 2{e^2} = 8$
$ \Rightarrow {e^2} = 4$
Now take square root we have,
$ \Rightarrow e = \pm 2$
$ \Rightarrow e = f = \pm 2$
So the focus of the parabola is $\left( {2,2} \right)$ or (-2, -2)
Therefore there are two parabolas possible one with vertex and focus are (1, 1) and (2, 2) respectively lying in the first quadrant.
And other parabola with vertex and focus are (-1, -1) and (-2, -2) respectively lying in the third quadrant.
So the distance (a) between the vertex and the focus of the parabola is
$ \Rightarrow a = \sqrt {{{\left( {f - d} \right)}^2} + {{\left( {e - c} \right)}^2}} $
Now substitute the values for the first case we have,
$ \Rightarrow a = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2 $
And for the second case
$a = \sqrt {{{\left( { - 2 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 2 - \left( { - 1} \right)} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2 $
So the directrix of the parabola is behind the vertex at distance (a) for first case and in front of vertex for second case.
So as we see that the distance (a) is the same as the distance from the origin and the vertex.
Therefore the directrix of the parabola passes through the origin and perpendicular to the axis of the parabola as shown in the figure (as the directrix is always perpendicular to the axis of the parabola).
So the equation of the directrix is
$ \Rightarrow y = - x$
$ \Rightarrow y + x = 0$
Now according to parabola property the distance from the focus (2, 2) of the parabola to any general point P (x, y) on the parabola and the perpendicular distance from the point P to the directrix is equal.
Therefore,
$ \Rightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 2} \right)}^2}} = \left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|$, [as the perpendicular distance from point (${x_1},{y_1}$) on general equation ax +by + c = 0 is given as$\dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$]
Now simplify the above equation by squaring on both sides we have,
$ \Rightarrow {\left( {\sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 2} \right)}^2}} } \right)^2} = {\left( {\left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|} \right)^2}$
$ \Rightarrow {x^2} + 4 - 4x + {y^2} + 4 - 4y = \dfrac{{{{\left( {x + y} \right)}^2}}}{2}$
$ \Rightarrow 2{x^2} + 8 - 8x + 2{y^2} + 8 - 8y = {x^2} + {y^2} + 2xy$
$ \Rightarrow {x^2} + {y^2} - 2xy = 8x + 8y - 16$
$ \Rightarrow {\left( {x - y} \right)^2} = 8\left( {x + y - 2} \right)$
So this is the required equation of the parabola.
For the second case the distance from the focus (-2, -2) of the parabola to any general point P (x, y) on the parabola and the perpendicular distance from the point P to the directrix is equal.
Therefore,
$ \Rightarrow \sqrt {{{\left( {x - \left( { - 2} \right)} \right)}^2} + {{\left( {y - \left( { - 2} \right)} \right)}^2}} = \left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|$, [as the perpendicular distance from point (${x_1},{y_1}$) on general equation ax +by + c = 0 is given as$\dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$]
Now simplify the above equation by squaring on both sides we have,
$ \Rightarrow {\left( {\sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y + 2} \right)}^2}} } \right)^2} = {\left( {\left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|} \right)^2}$
$ \Rightarrow {x^2} + 4 + 4x + {y^2} + 4 + 4y = \dfrac{{{{\left( {x + y} \right)}^2}}}{2}$
$ \Rightarrow 2{x^2} + 8 + 8x + 2{y^2} + 8 + 8y = {x^2} + {y^2} + 2xy$
$ \Rightarrow {x^2} + {y^2} - 2xy = - 8x - 8y - 16$
$ \Rightarrow {\left( {x - y} \right)^2} = - 8\left( {x + y + 2} \right)$
So this is also the required equation of the parabola.
So in the given options only option (A) is matching
Hence option (A) is the correct answer.
Note – The general equation of any conic section is given as $a{x^2} + bxy + c{y^2} + dx + ey + f = 0$where a, b, c, d, e and f are arbitrary constants. The value of these arbitrary constants directly influence the shape of the conic section that is being taken into consideration. So we need to be confused that the standard equation of parabola is only of the form${y^2} = 4ax{\text{ or }}{{\text{x}}^2} = 4ay$. Thus if we expand the option (a) which is the right answer a more general equation of conic section is obtained.
Complete step-by-step answer:
It is given that the axis of the parabola is y = x.
And the vertex of the parabola is $\sqrt 2 $ from the origin.
Let the coordinates of the vertex of the parabola be (c, d).
The distance between any two pair of points $({x_1},{y_1}){\text{ and (}}{{\text{x}}_2},{y_2}){\text{ is }}\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
So the distance between origin (0, 0) and (c, d) is $\sqrt 2 $
$ \Rightarrow \sqrt 2 = \sqrt {{{\left( {d - 0} \right)}^2} + {{\left( {c - 0} \right)}^2}} $
Now squaring on both sides we have,
$ \Rightarrow 2 = {\left( d \right)^2} + {\left( c \right)^2}$
It is given that the axis of the parabola is y = x, as the vertex lies on the axis therefore, c = d.
$ \Rightarrow {c^2} + {c^2} = 2$
$ \Rightarrow 2{c^2} = 2$
$ \Rightarrow {c^2} = 1$
Now take square root we have,
$ \Rightarrow c = \pm 1$
$ \Rightarrow c = d = \pm 1$
So the vertex of the parabola is (1, 1) or (-1, -1)
Now it is also given that the distance of the focus of the parabola from the origin is$2\sqrt 2 $.
Let the coordinates of the focus of the parabola be (e, f).
So the distance between origin (0, 0) and (e, f) is $2\sqrt 2 $
$ \Rightarrow 2\sqrt 2 = \sqrt {{{\left( {f - 0} \right)}^2} + {{\left( {e - 0} \right)}^2}} $
Now squaring on both sides we have,
$ \Rightarrow {\left( {2\sqrt 2 } \right)^2} = {\left( e \right)^2} + {\left( f \right)^2}$
$ \Rightarrow {e^2} + {f^2} = 8$
It is given that the axis of the parabola is y = x, as the vertex is also lying on the axis therefore, e = f
$ \Rightarrow {e^2} + {e^2} = 8$
$ \Rightarrow 2{e^2} = 8$
$ \Rightarrow {e^2} = 4$
Now take square root we have,
$ \Rightarrow e = \pm 2$
$ \Rightarrow e = f = \pm 2$
So the focus of the parabola is $\left( {2,2} \right)$ or (-2, -2)
Therefore there are two parabolas possible one with vertex and focus are (1, 1) and (2, 2) respectively lying in the first quadrant.
And other parabola with vertex and focus are (-1, -1) and (-2, -2) respectively lying in the third quadrant.
So the distance (a) between the vertex and the focus of the parabola is
$ \Rightarrow a = \sqrt {{{\left( {f - d} \right)}^2} + {{\left( {e - c} \right)}^2}} $
Now substitute the values for the first case we have,
$ \Rightarrow a = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2 $
And for the second case
$a = \sqrt {{{\left( { - 2 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 2 - \left( { - 1} \right)} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2 $
So the directrix of the parabola is behind the vertex at distance (a) for first case and in front of vertex for second case.
So as we see that the distance (a) is the same as the distance from the origin and the vertex.
Therefore the directrix of the parabola passes through the origin and perpendicular to the axis of the parabola as shown in the figure (as the directrix is always perpendicular to the axis of the parabola).
So the equation of the directrix is
$ \Rightarrow y = - x$
$ \Rightarrow y + x = 0$
Now according to parabola property the distance from the focus (2, 2) of the parabola to any general point P (x, y) on the parabola and the perpendicular distance from the point P to the directrix is equal.
Therefore,
$ \Rightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 2} \right)}^2}} = \left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|$, [as the perpendicular distance from point (${x_1},{y_1}$) on general equation ax +by + c = 0 is given as$\dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$]
Now simplify the above equation by squaring on both sides we have,
$ \Rightarrow {\left( {\sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 2} \right)}^2}} } \right)^2} = {\left( {\left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|} \right)^2}$
$ \Rightarrow {x^2} + 4 - 4x + {y^2} + 4 - 4y = \dfrac{{{{\left( {x + y} \right)}^2}}}{2}$
$ \Rightarrow 2{x^2} + 8 - 8x + 2{y^2} + 8 - 8y = {x^2} + {y^2} + 2xy$
$ \Rightarrow {x^2} + {y^2} - 2xy = 8x + 8y - 16$
$ \Rightarrow {\left( {x - y} \right)^2} = 8\left( {x + y - 2} \right)$
So this is the required equation of the parabola.
For the second case the distance from the focus (-2, -2) of the parabola to any general point P (x, y) on the parabola and the perpendicular distance from the point P to the directrix is equal.
Therefore,
$ \Rightarrow \sqrt {{{\left( {x - \left( { - 2} \right)} \right)}^2} + {{\left( {y - \left( { - 2} \right)} \right)}^2}} = \left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|$, [as the perpendicular distance from point (${x_1},{y_1}$) on general equation ax +by + c = 0 is given as$\dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$]
Now simplify the above equation by squaring on both sides we have,
$ \Rightarrow {\left( {\sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y + 2} \right)}^2}} } \right)^2} = {\left( {\left| {\dfrac{{x + y}}{{\sqrt {{1^2} + {1^2}} }}} \right|} \right)^2}$
$ \Rightarrow {x^2} + 4 + 4x + {y^2} + 4 + 4y = \dfrac{{{{\left( {x + y} \right)}^2}}}{2}$
$ \Rightarrow 2{x^2} + 8 + 8x + 2{y^2} + 8 + 8y = {x^2} + {y^2} + 2xy$
$ \Rightarrow {x^2} + {y^2} - 2xy = - 8x - 8y - 16$
$ \Rightarrow {\left( {x - y} \right)^2} = - 8\left( {x + y + 2} \right)$
So this is also the required equation of the parabola.
So in the given options only option (A) is matching
Hence option (A) is the correct answer.
Note – The general equation of any conic section is given as $a{x^2} + bxy + c{y^2} + dx + ey + f = 0$where a, b, c, d, e and f are arbitrary constants. The value of these arbitrary constants directly influence the shape of the conic section that is being taken into consideration. So we need to be confused that the standard equation of parabola is only of the form${y^2} = 4ax{\text{ or }}{{\text{x}}^2} = 4ay$. Thus if we expand the option (a) which is the right answer a more general equation of conic section is obtained.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success
Glucose when reduced with HI and red Phosphorus gives class 11 chemistry CBSE
The highest possible oxidation states of Uranium and class 11 chemistry CBSE
Find the value of x if the mode of the following data class 11 maths CBSE
Which of the following can be used in the Friedel Crafts class 11 chemistry CBSE
A sphere of mass 40 kg is attracted by a second sphere class 11 physics CBSE
Trending doubts
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
State and prove Bernoullis theorem class 11 physics CBSE
What organs are located on the left side of your body class 11 biology CBSE
How many valence electrons does nitrogen have class 11 chemistry CBSE