Question

The base edge of a regular pentagonal prism is $6\text{ cm}$ and its bases are $12\text{ cm}$ apart. Find its volume in cu.cm.
(a) 743.22
(b) 786.89
(c) 567.45
(d) 842.12

Answer 1

Hint: For solving this question first we will see the figure of the given prism and then we will find the area of the base by using some basic geometrical techniques. After that, we will find the volume of the regular pentagon by multiplying the area of the base with the height and select the correct option.
Complete step-by-step answer:
Given:
We have to find the volume of a regular pentagonal prism whose height is of 12 cm and the base edge is of 6 cm. For more clarity look at the figure given below:

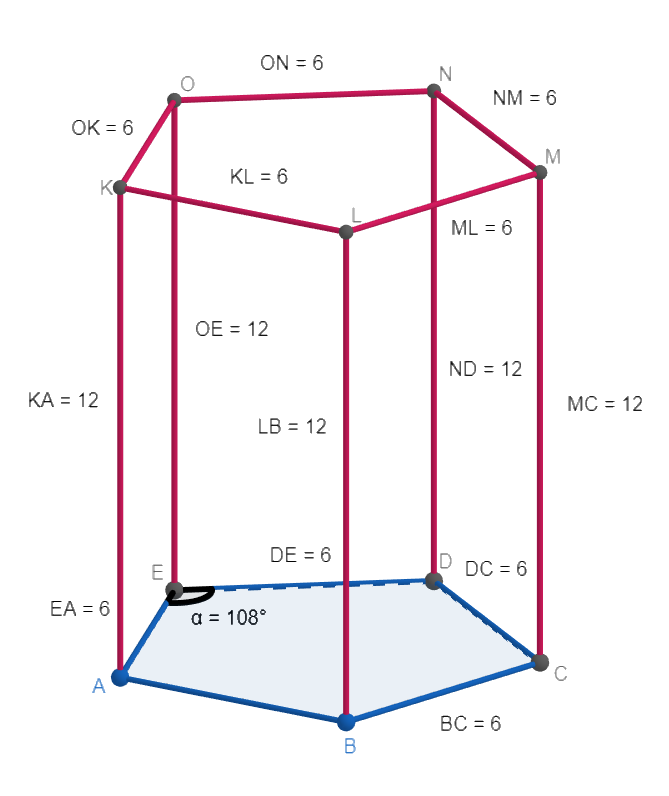
In the above figure, we have a regular pentagonal prism whose height is of 12 cm and the base edge is of 6 cm.
Now, to find the volume we will find the area of the base and multiply it with a height of 12 cm. And the base will be a regular pentagon of edge 6 cm.
Now, we will draw a regular pentagon of edge length 6 cm and try to find its area. We will join every vertex of the pentagon to its centre then, we will get five isosceles triangles. For more clarity look at the figure given below:

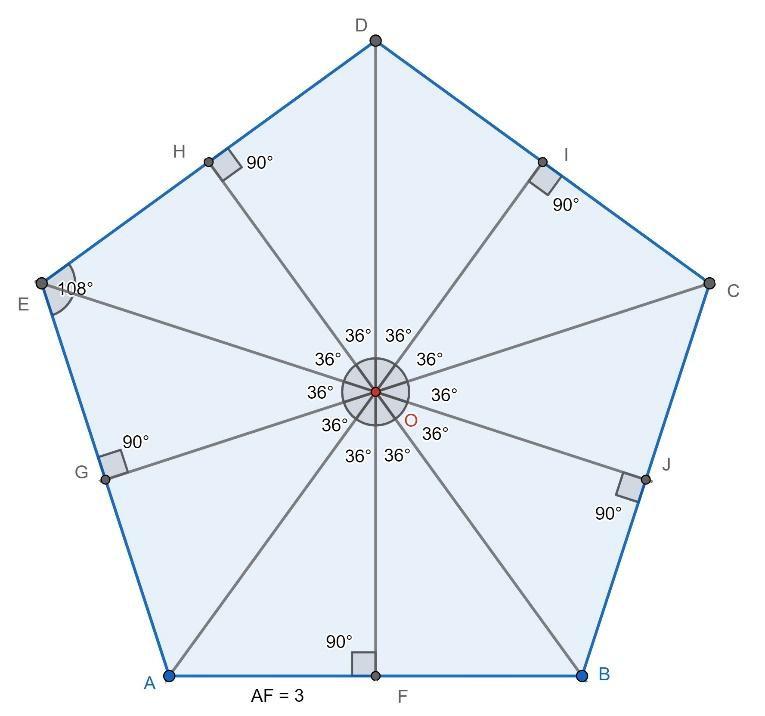
Now, from the above figure we conclude that area of the regular pentagon $ABCDE$ will be equal to the addition of the area of $\Delta AOB$ , $\Delta BOC$ , $\Delta COD$ , $\Delta DOE$ and $\Delta EOA$ .
Now, consider $\Delta AOB$ OF will be the perpendicular bisector of the side AB and value of $\angle AOF=\dfrac{{{360}^{\circ}}}{10}={{36}^{\circ}}$ and length of $AF=3$ .
Now, we should know the value of $\tan {{36}^{\circ}}$ .
Now, before we proceed we should know the following formulas:
$\begin{align}
  & \sin \left( {{90}^{\circ}}-\theta \right)=\cos \theta ...........................\left( 1 \right) \\
 & \sin 2\theta =2\sin \theta \cos \theta ...........................\left( 2 \right) \\
 & \cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta ...................\left( 3 \right) \\
 & a{{x}^{2}}+bx=c=0 \\
 & x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}...........................\left( 4 \right) \\
 & \cos 2\theta =1-2{{\sin }^{2}}\theta ............................\left( 5 \right) \\
 & {{\tan }^{2}}\theta +1=\dfrac{1}{{{\cos }^{2}}\theta }.............................\left( 6 \right) \\
\end{align}$
Now, let $\theta ={{18}^{\circ}}$ . Then,
$\begin{align}
  & \theta ={{18}^{\circ}} \\
 & \Rightarrow 5\theta ={{90}^{\circ}} \\
 & \Rightarrow 2\theta +3\theta ={{90}^{\circ}} \\
 & \Rightarrow 2\theta ={{90}^{\circ}}-3\theta \\
 & \Rightarrow \sin 2\theta =\sin \left( {{90}^{\circ}}-3\theta \right) \\
\end{align}$
Now, using the formula form the equation (1), (2) and (3). Then,
$\begin{align}
  & \sin 2\theta =\sin \left( {{90}^{\circ}}-3\theta \right) \\
 & \Rightarrow 2\sin \theta \cos \theta =\cos 3\theta \\
 & \Rightarrow 2\sin \theta \cos \theta =4{{\cos }^{3}}\theta -3\cos \theta \\
 & \Rightarrow \cos \theta \left( 2\sin \theta +3-4{{\cos }^{2}}\theta \right)=0 \\
\end{align}$
Now, as $\cos \theta =\cos {{18}^{\circ}}\ne 0$ and ${{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta $ . Then,
$\begin{align}
  & \cos \theta \left( 2\sin \theta +3-4{{\cos }^{2}}\theta \right)=0 \\
 & \Rightarrow 2\sin \theta +3-4{{\cos }^{2}}\theta =0 \\
 & \Rightarrow 2\sin \theta +3-4+4{{\sin }^{2}}\theta =0 \\
 & \Rightarrow 4{{\sin }^{2}}\theta +2\sin \theta -1=0 \\
\end{align}$
Now, using the formula from the equation (4). Then,
$\begin{align}
  & 4{{\sin }^{2}}\theta +2\sin \theta -1=0 \\
 & \Rightarrow \sin \theta =\dfrac{-2\pm \sqrt{4+16}}{8} \\
 & \Rightarrow \sin \theta =\dfrac{-2\pm \sqrt{20}}{8} \\
 & \Rightarrow \sin \theta =\dfrac{-2\pm 2\sqrt{5}}{8} \\
 & \Rightarrow \sin \theta =\dfrac{-1\pm \sqrt{5}}{4} \\
\end{align}$
Now, as $\sin \theta =\sin {{18}^{\circ}}>0$ . Then,
$\begin{align}
  & \sin \theta =\dfrac{-1\pm \sqrt{5}}{4} \\
 & \Rightarrow \sin \theta =\dfrac{\sqrt{5}-1}{4} \\
\end{align}$
Now, as we got $\sin \theta =\sin {{18}^{\circ}}=\dfrac{\sqrt{5}-1}{4}$ so, we will use the formula from the equation (5). Then,
$\begin{align}
  & \cos 2\theta =1-2{{\sin }^{2}}\theta \\
 & \Rightarrow \cos {{36}^{\circ}}=1-2{{\sin }^{2}}{{18}^{\circ}} \\
 & \Rightarrow \cos {{36}^{\circ}}=1-2{{\left( \dfrac{\sqrt{5}-1}{4} \right)}^{2}} \\
 & \Rightarrow \cos {{36}^{\circ}}=1-2\left( \dfrac{5+1-2\sqrt{5}}{16} \right) \\
 & \Rightarrow \cos {{36}^{\circ}}=1-\dfrac{6-2\sqrt{5}}{8} \\
 & \Rightarrow \cos {{36}^{\circ}}=\dfrac{8-6+2\sqrt{5}}{8} \\
 & \Rightarrow \cos {{36}^{\circ}}=\dfrac{2+2\sqrt{5}}{8} \\
 & \Rightarrow \cos {{36}^{\circ}}=\dfrac{1+\sqrt{5}}{4} \\
 & \Rightarrow \dfrac{1}{\cos {{36}^{\circ}}}=\dfrac{4}{1+\sqrt{5}} \\
 & \Rightarrow \dfrac{1}{\cos {{36}^{\circ}}}=\dfrac{4}{\left( \sqrt{5}+1 \right)}\times \dfrac{\left( \sqrt{5}-1 \right)}{\left( \sqrt{5}-1 \right)} \\
 & \Rightarrow \dfrac{1}{\cos {{36}^{\circ}}}=\dfrac{4}{\left( 5-1 \right)}\times \left( \sqrt{5}-1 \right) \\
 & \Rightarrow \dfrac{1}{\cos {{36}^{\circ}}}=\sqrt{5}-1 \\
\end{align}$
Now, using the formula from the equation (6). Then,
$\begin{align}
  & {{\tan }^{2}}\theta +1=\dfrac{1}{{{\cos }^{2}}\theta } \\
 & \Rightarrow {{\tan }^{2}}{{36}^{\circ}}+1=\dfrac{1}{{{\cos }^{2}}{{36}^{\circ}}} \\
 & \Rightarrow {{\tan }^{2}}{{36}^{\circ}}+1={{\left( \sqrt{5}-1 \right)}^{2}} \\
 & \Rightarrow {{\tan }^{2}}{{36}^{\circ}}+1=5+1-2\sqrt{5} \\
 & \Rightarrow {{\tan }^{2}}{{36}^{\circ}}=5-2\sqrt{5} \\
 & \Rightarrow \tan {{36}^{\circ}}=\sqrt{5-2\sqrt{5}}....................\left( 7 \right) \\
\end{align}$
Now, we come back to our question. First look at the figure given below:

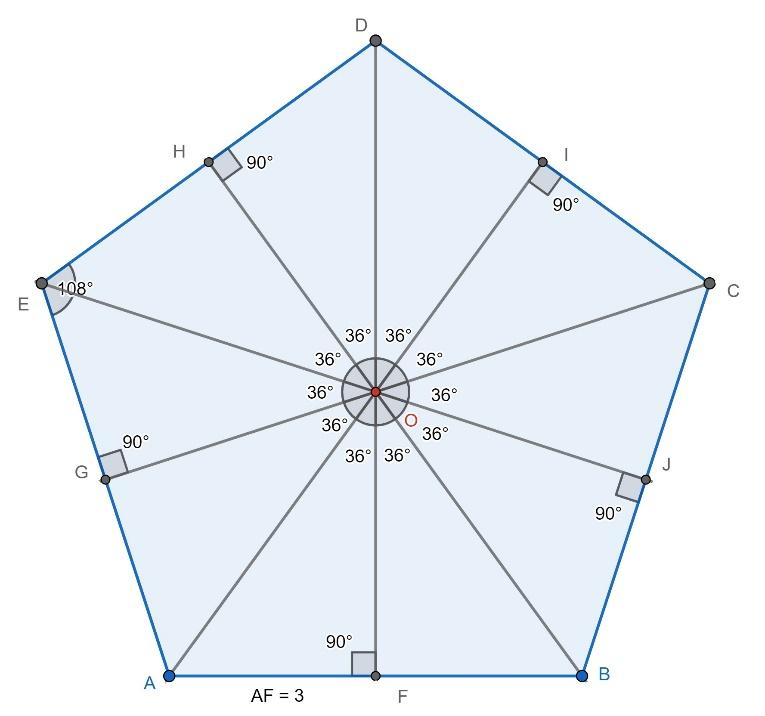
Now, consider $\Delta AOB$ OF will be the perpendicular bisector of the side AB and value of $\angle AOF=\dfrac{{{360}^{\circ}}}{10}={{36}^{\circ}}$ and length of $AF=3$ . Then,
$\begin{align}
  & \tan \left( \angle AOF \right)=\dfrac{\left( \text{length of the perpendicular AF} \right)}{\left( \text{length of the base OF} \right)} \\
 & \Rightarrow \tan {{36}^{\circ}}=\dfrac{AF}{OF} \\
\end{align}$
Now, put the value of $\tan {{36}^{\circ}}=\sqrt{5-2\sqrt{5}}$ from the equation (7) in the above equation. Then,
$\begin{align}
  & \tan {{36}^{\circ}}=\dfrac{AF}{OF} \\
 & \Rightarrow \sqrt{5-2\sqrt{5}}=\dfrac{3}{OF} \\
 & \Rightarrow OF=\dfrac{3}{\sqrt{5-2\sqrt{5}}} \\
\end{align}$
Now, in the $\Delta AOB$ length of the base $AB=6$ and height $OF=\dfrac{3}{\sqrt{5-2\sqrt{5}}}$ . Then,
$\begin{align}
  & Are{{a}_{\Delta AOB}}=\dfrac{1}{2}\left( base \right)\left( height \right) \\
 & \Rightarrow Are{{a}_{\Delta AOB}}=\dfrac{1}{2}\times 6\times \dfrac{3}{\sqrt{5-2\sqrt{5}}} \\
 & \Rightarrow Are{{a}_{\Delta AOB}}=\dfrac{9}{\sqrt{5-2\sqrt{5}}} \\
\end{align}$
Now, as the area of $\Delta AOB$ , $\Delta BOC$ , $\Delta COD$ , $\Delta DOE$ and $\Delta EOA$ will be equal. Then,
$\begin{align}
  & Are{{a}_{Pentagon\text{ }ABCDE}}=5\times Are{{a}_{\Delta AOB}} \\
 & \Rightarrow Are{{a}_{Pentagon\text{ }ABCDE}}=5\times \dfrac{9}{\sqrt{5-2\sqrt{5}}} \\
 & \Rightarrow Are{{a}_{Pentagon\text{ }ABCDE}}=\dfrac{45}{\sqrt{5-2\sqrt{5}}} \\
\end{align}$
Now, we know that the volume of the pentagonal prism will be the area of the base multiplied with the height of 12 cm. Then,
$\begin{align}
  & Volum{{e}_{Pentagonal\text{ }\Pr ism}}=Are{{a}_{Pentagon\text{ }ABCDE}}\times 12 \\
 & \Rightarrow Volum{{e}_{Pentagonal\text{ }\Pr ism}}=\dfrac{45}{\sqrt{5-2\sqrt{5}}}\times 12 \\
 & \Rightarrow Volum{{e}_{Pentagonal\text{ }\Pr ism}}=\dfrac{540}{\sqrt{5-2\sqrt{5}}} \\
 & \Rightarrow Volum{{e}_{Pentagonal\text{ }\Pr ism}}\approx 743.246 \\
\end{align}$
Now, from the above result, we conclude that the volume of the given pentagonal prism will be 743.246 cu.cm approximately.
Hence, (a) will be the correct option.
Note: Here, the student should first understand what is asked in the problem and then proceed in the right direction. After that, we should solve correctly to get the correct result. Moreover, for the objective question to get the answer quickly we should apply the direct formula $1.7204\times {{a}^{2}}\times h$ for the volume of a pentagonal prism whose base is of a regular pentagon of edge $a$ units and height is of $h$ units.