Question

The base radii of two circular cones of the same height are in the ratio \[3:5\]. Find the ratio of their volumes.

Answer 1

Hint: First we will use the formula of volume of a cone is \[\dfrac{1}{3}\pi {r^2}h\], where \[r\] is the radius of the base of the cone and \[h\] is the height and then assume that \[{r_1}\] be the radius of the first cone and \[h\] is the height of the first cone and \[{r_2}\] is the radius of the second cone and \[h\] is the height of the second cone. Then we will write the ratio of the volumes of the first cone and the second cone by using the formula of volume of cones and after substituting the value of the ratio \[{r_1}:{r_2}\] in the above expression to find the required value.

Complete step by step answer:

We are given that the base radii of two circular cones of the same height are in the ratio \[3:5\].
First, we will use the formula of volume of a cone is \[\dfrac{1}{3}\pi {r^2}h\], where \[r\] is the radius of the base of the cone and \[h\] is the height.

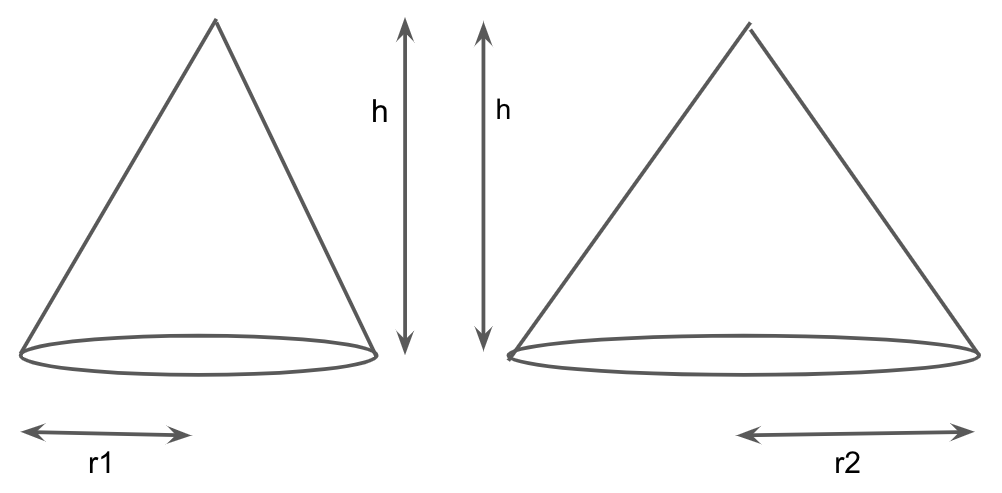
Since height is the same for the two cones, let us assume that \[{r_1}\] be the radius of the first cone and \[h\] is the height of the first cone and \[{r_2}\] is the radius of the second cone and \[h\] is the height of the second cone.

Now, writing the ratio of the volumes of the first cone and the second cone by using the formula of volume of cones.

\[
   \Rightarrow \dfrac{1}{3}\pi {r_1}^2h:\dfrac{1}{3}\pi {r_2}^2h \\
   \Rightarrow {r_1}^2:{r_2}^2 \\
   \Rightarrow {\left( {{r_1}:{r_2}} \right)^2} \\
 \]

Substituting the value of the ratio \[{r_1}:{r_2}\] in the above expression, we get
\[
   \Rightarrow {\left( {3:5} \right)^2} \\
   \Rightarrow {3^2}:{5^2} \\
   \Rightarrow 9:25 \\
 \]

Thus, the volumes are in the ratio is \[9:25\].

Note: In solving these types of questions, students need to know the key concept is that they always have to remember the formula of a cone which is stated above, then using this formula to calculate the ratio of volume two cones and simplify to get the answer. Students may go wrong like they may think that they do not have the value of \[h\] and they cannot solve it.