
The
a)
b)
c)
d) None of these

Answer
494.7k+ views
2 likes
Hint: B-H curve shows that a given material doesn’t not follow the same path during magnetization and demagnetization. This creates a difference in the current, which is responsible for reduction of magnetization of the material. The current, at which the current demagnetizes, no longer remains zero but has a negative value. We will use this concept along with the basic formula to find the answer.
Formula used:
Complete step by step answer:
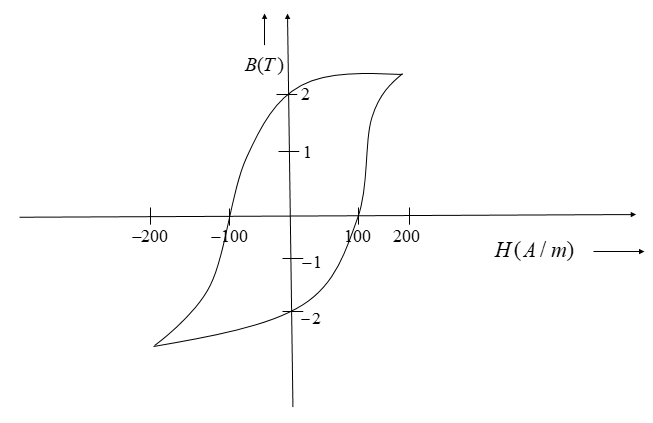
The B-H curve represents the magnetization and demagnetization characteristics of a ferromagnetic material. It shows the amount of current required for a particular magnetization to be achieved. It also shows that for a given ferromagnetic material, the path traced during magnetization and demagnetization are not the same.
We know that the magnetic intensity has a unique relation with the current passing through the conducting wire along with the number turns. This relation is as follows:
Where,
We can modify the above equation as:
Here, it can be clearly seen that for the complete demagnetization of the ferromagnetic material, the y-axis component must be zero, i.e.,
Putting this value of
So, the correct answer is “Option B”.
Note: Don’t panic when length is not mentioned in such questions. Generally, the length is already present in other parameters often disguised. For example, here length was present in the
Formula used:
Complete step by step answer:
The B-H curve represents the magnetization and demagnetization characteristics of a ferromagnetic material. It shows the amount of current required for a particular magnetization to be achieved. It also shows that for a given ferromagnetic material, the path traced during magnetization and demagnetization are not the same.
We know that the magnetic intensity has a unique relation with the current passing through the conducting wire along with the number turns. This relation is as follows:
Where,
We can modify the above equation as:
Here, it can be clearly seen that for the complete demagnetization of the ferromagnetic material, the y-axis component must be zero, i.e.,
Putting this value of
So, the correct answer is “Option B”.
Note: Don’t panic when length is not mentioned in such questions. Generally, the length is already present in other parameters often disguised. For example, here length was present in the
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




