Question

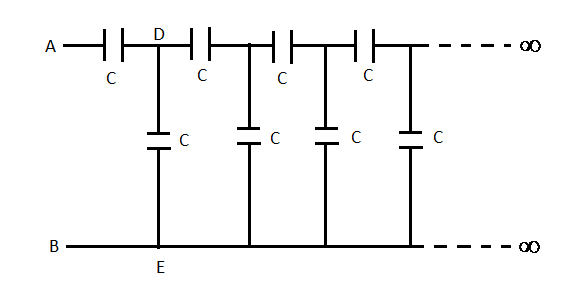
The capacitance of an infinite circuit formed by the repetition of the same link consisting of two identical capacitors, each with capacitance $C$ as shown in the figure is:

A) Zero
$B)\text{ }\dfrac{\sqrt{5}-1}{2}C$
$C)\text{ }\dfrac{\sqrt{5}+1}{2}C$
D) infinite

Answer 1

Hint: This problem can be solved by considering the circuit to be a series combination of the first capacitor in the first link with the parallel combination of the second capacitor in the first link and the rest of the circuit. The parallel combination must be equal to the equivalent capacitance of the circuit since the same portion of the circuit is repeating till infinity and anything added to infinity is infinity.

Formula used:
${{C}_{parallel,eq}}=\sum\limits_{i=1}^{n}{{{C}_{i}}}$
$\dfrac{1}{{{C}_{series,eq}}}=\sum\limits_{i=1}^{n}{\dfrac{1}{{{C}_{i}}}}$

Complete step by step answer:
Upon close observation of the circuit, we can see that it is a repetition of the same link containing two capacitors which extends up to infinity. Now, the equivalent capacitance of the circuit can be written as the equivalent capacitance of the series combination of the first capacitor and the parallel combination of the second capacitor and the rest of the circuit. Since, the circuit extends till infinity, the equivalent capacitance of the rest of the circuit is equal to the equivalent capacitance of the total circuit (since anything added to infinity is infinity).
Therefore, the circuit can be redrawn as

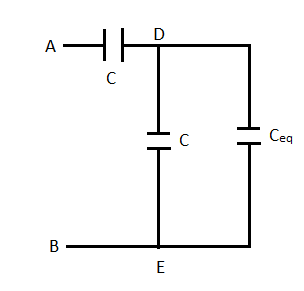
As explained earlier ${{C}_{eq}}$ is the equivalent capacitance of the total circuit and can be approximated to be the equivalent capacitance of all the repeated links other than the first link.
From this figure we can see that the equivalent capacitance of the circuit is the capacitance of the series combination of the capacitor between A and D with the parallel combination of the capacitor between D and E and ${{C}_{eq}}$.
$\therefore {{C}_{eq}}=C+\left( C||{{C}_{eq}} \right)$
Now, the equivalent capacitance ${{C}_{series,eq}}$ of $n$ capacitors in series with capacitances ${{C}_{i}}\left( i=1,2....n \right)$ is given by
$\dfrac{1}{{{C}_{series,eq}}}=\sum\limits_{i=1}^{n}{\dfrac{1}{{{C}_{i}}}}$ --(2)
Now, the equivalent capacitance ${{C}_{parallel,eq}}$ of $n$ capacitors in parallel with capacitances ${{C}_{i}}\left( i=1,2....n \right)$ is given by
${{C}_{parallel,eq}}=\sum\limits_{i=1}^{n}{{{C}_{i}}}$ --(3)
Now, using (3), we get
$C||{{C}_{eq}}=C+{{C}_{eq}}$ -- (4)
Now, using (2), we get
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{C}+\dfrac{1}{C||{{C}_{eq}}}$
Putting (4) in the above equation, we get
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{C}+\dfrac{1}{C+{{C}_{eq}}}=\dfrac{C+{{C}_{eq}}+C}{C\left( C+{{C}_{eq}} \right)}=\dfrac{2C+{{C}_{eq}}}{C\left( C+{{C}_{eq}} \right)}$
$\Rightarrow C\left( C+{{C}_{eq}} \right)={{C}_{eq}}\left( 2C+{{C}_{eq}} \right)$
$\Rightarrow {{C}^{2}}+C.{{C}_{eq}}=2C.{{C}_{eq}}+{{C}_{eq}}^{2}$
$\Rightarrow {{C}_{eq}}^{2}+C.{{C}_{eq}}-{{C}^{2}}=0$
$\Rightarrow {{C}_{eq}}=\dfrac{-C\pm \sqrt{{{C}^{2}}-4\left( 1 \right)\left( -{{C}^{2}} \right)}}{2\left( 1 \right)}$ $\left( \because \text{if }a{{x}^{2}}+bx+c=0,x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \right)$
$\Rightarrow {{C}_{eq}}=\dfrac{-C\pm \sqrt{{{C}^{2}}+4{{C}^{2}}}}{2}=\dfrac{-C\pm \sqrt{5{{C}^{2}}}}{2}=\dfrac{-C\pm C\sqrt{5}}{2}=\dfrac{C\left( -1\pm \sqrt{5} \right)}{2}$
$\Rightarrow {{C}_{eq}}=\dfrac{C\left( \sqrt{5}-1 \right)}{2}$ $\left( {{C}_{eq}}\ne \left( \dfrac{-1-\sqrt{5}}{2}C \right),\because {{C}_{eq}}\text{ cannot be negative} \right)$
$\therefore {{C}_{eq}}=\dfrac{\sqrt{5}-1}{2}C$
Therefore, the correct option is $B)\text{ }\dfrac{\sqrt{5}-1}{2}C$.

Note:
Students can make the mistake of thinking that the equivalent capacitance will be the series combination of the first two capacitance in the first link and the equivalent capacitance of the rest of the links. This can be the first thought striking the minds of many students since they may think that since the same link is being repeated, it must be a series combination of each link extending up till infinity. However, as seen in the answer, this is not true and will not give the equivalent capacitance of the circuit in between the desired points.