Question

What can be the causes of helical motion of a charged particle?

Answer 1

Hint: When a charged particle moves inside a magnetic field, it experiences a force which is perpendicular to both the magnetic field and velocity. If the velocity of the particle is at an angle with the magnetic field, the force due to the magnetic field can be divided into two components. These components help in maintaining a circular motion and having a displacement as well.

Complete step by step answer:
Let us first look into phenomenon when the magnetic field is perpendicular to the motion of the charged particle.

The following diagram shows the phenomenon.

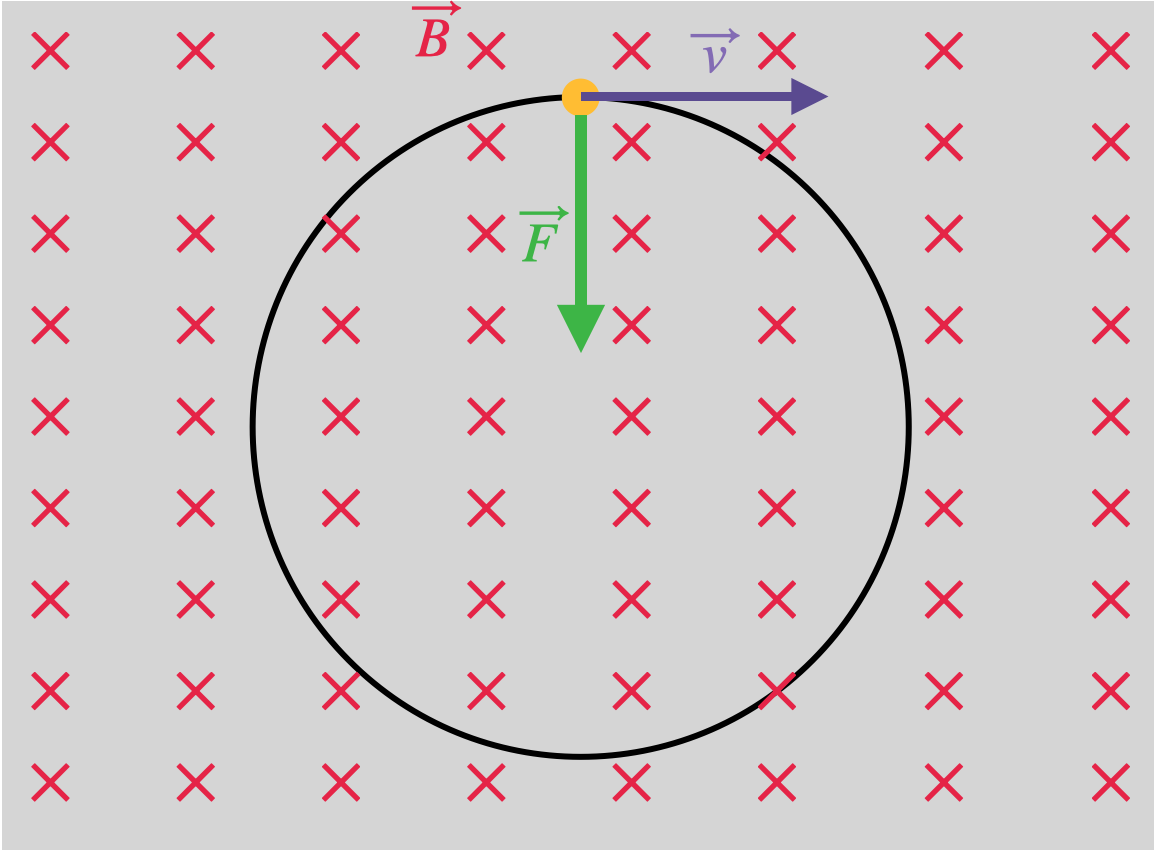
In this diagram, the charged particle is a negatively charged electron. Using Fleming's right-hand rule, we can check that the force due to the magnetic field is towards the centre of the circle. This force helps the particle maintain a circular motion.

However, when the velocity of the charged particle is not perpendicular to the magnetic field the force also does not work directly towards the centre of the circle.

Look at the following diagrams to understand the concept clearly.

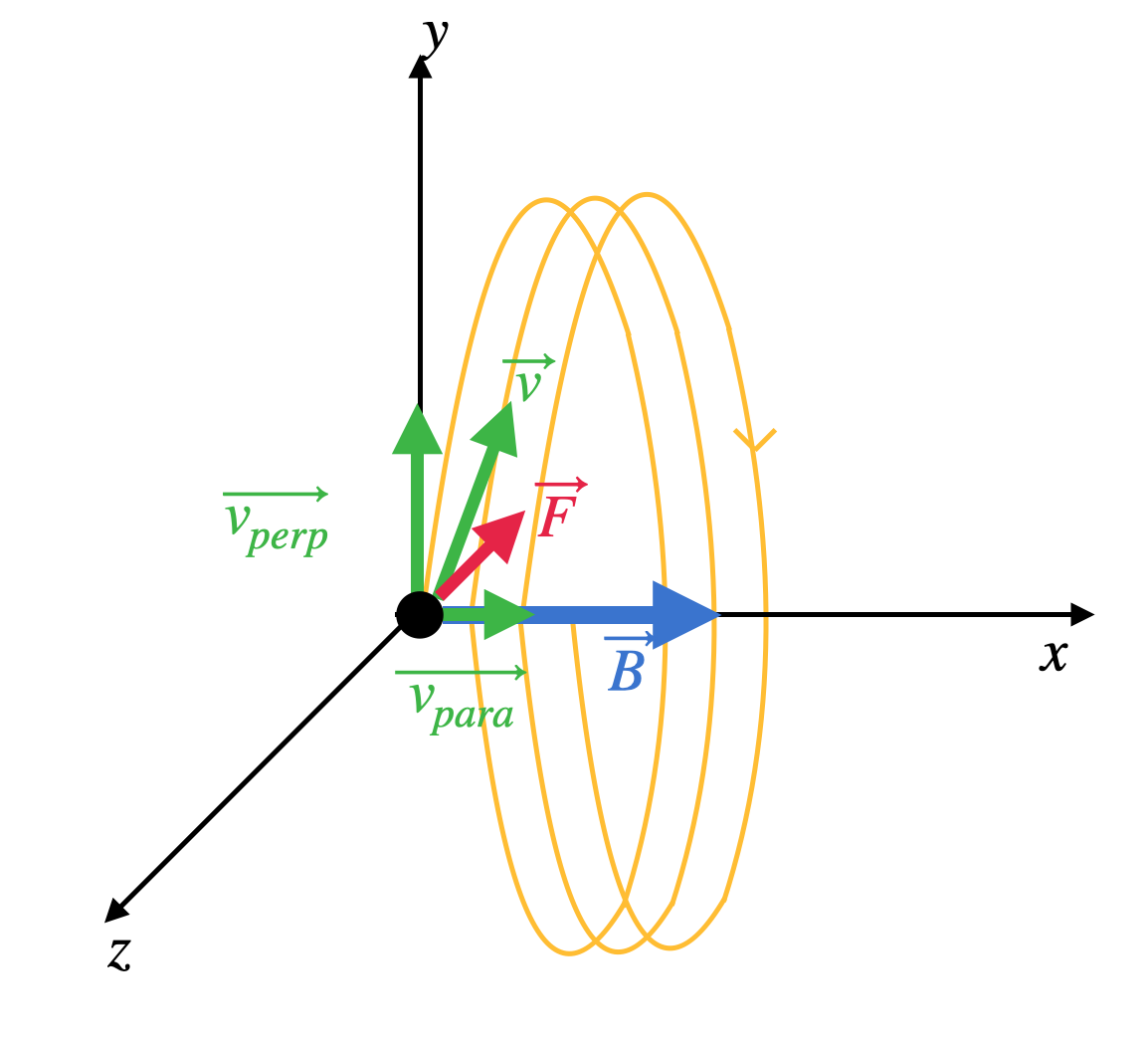
As the velocity of the particle is not perpendicular to the magnetic field, we can divide the velocity in two perpendicular components. These components are as follows:
${{v}_{perp}}=v\sin \theta $
${{v}_{para}}=v\cos \theta $

If we look closely, the perpendicular component will help the particle to maintain a circular path because of the force. The force is acting directly towards the centre of the circle at that instant.
The parallel component will not change because the magnetic field has no effect on a charged particle moving along the magnetic field. Hence, it will follow a helix pattern.

This is the reason why a charged particle can follow a helix pattern in the presence of a magnetic field.

Note: We can calculate the properties of the helix by measuring the velocity components. The radius of the helix will be given by,
$r=\dfrac{mv\sin \theta }{qB}$
And, the pitch of the helix will be given by,
$pitch=(v\cos \theta )(\dfrac{2\pi m}{qB})$

You should be well aware that the force is a cross product of velocity and magnetic field. In that way, you can determine the direction of the force. You need to incorporate the polarity of the charge as well.