Question

The ciliary muscles of eye control the curvature of the lens in the eye and hence and alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of the lens increases. That means, the radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and equals the distance of retina from the eye lens. It is about 2.5cm for a grown up person.
A person can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are more strained in this position. For an average grown up person, the minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens or spectacles is to form the image of the object within the range in which the person can see clearly. The image of the spectacle lens becomes an object for the eye lens and whose image is formed on the retina.
The number of spectacle lenses used for the remedy of eye defect is decided by the power of the lens required and the number of spectacle lenses is equal to the numerical value of the power of the lens with sign. For example, if the power of the lens required is +3D (converging lens of focal length 100/3 cm), then the number of lenses will be +3.
For all calculations required, you can use the lens formula and lens maker’s formula. Assume that the eye lens is an equi-convex lens. Neglect the distance between the eye lens and spectacle lens. A near sighted man can clearly see objects only up to a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will be,

A. +1
B. -1
C. +3
D. -3

Answer 1

Hint: The relationship between the image distance, object distance and the focal length is known as Lens law and it is applicable for both the types of the lenses.

Complete step by step answer:
The eye lens has the ability to change its focal length slightly through ciliary muscles. This permits us to focus the sharp image of the object at different distances from the eye at the retina. This property of the eye is called accommodation of the eye.
Let f be the focal length of the required concave lens and x be the distance of the far point from defect eye.
We have, $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Here we have$v = - x{\text{ and u = - }}\infty $
$\therefore \dfrac{1}{f} = \dfrac{1}{{ - x}} - \dfrac{1}{{ - \infty }}$
$\dfrac{1}{f} = \dfrac{1}{{ - x}}$
Therefore, focal length $f = - x$ .
The power of the required concave lens is $P = \dfrac{1}{f} = \dfrac{1}{{ - x}}$
Given, the power the lens should be such that the image of an object at infinity is obtained at a distance of 100cm = 1m by the lens.
From lens formula,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ \[\;\;\]
$\dfrac{1}{f} = \dfrac{1}{{ - 1}} - \dfrac{1}{{ - \infty }}$
${\text{Thus, Power = }}\dfrac{1}{f} = - 1$
Hence, the correct option is (B).

Additional information:
When the eye is focused on a distant object, the ciliary muscles are relaxed, so that the focal length of the eye lens increases, and an image is formed at the retina. When the eye is focused on a near object, the ciliary muscles contract and the focal length of the eye lens decreases. Thus, again a sharp image is focused at the retina.
The most distant point that the eye can see is called the far point of the eye. The closest point from the eye at which an object is seen is called the near point of the eye.
For a normal eye, the near point is at a distance of 25cm.
The light from a distant object arriving at the eye lens may get converged at a point in front of the retina. This type of defect is called short-sightedness or myopia. Due to this defect, the eye cannot see the distant object. Therefore, a human eye is short-sighted or myopic if it can see near objects clearly but is unable to see clearly the far-off objects. This defect is due to the increase in the size of the eyeball and the decrease in the focal length of the eye lens.

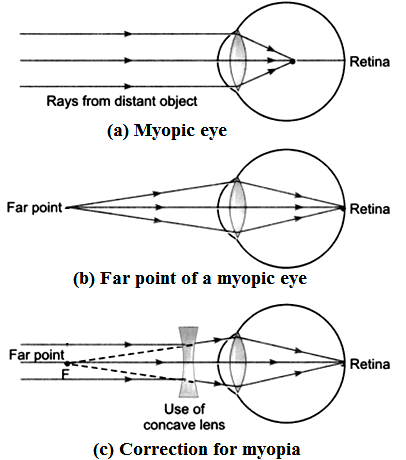
To correct short sighted vision, a concave lens of suitable focal length is placed in front of the eye.

Note: The lens formula is applicable for the problems involving the sign conventions. If the equation shows negative signs then the image is a virtual image.