
The condition for obtaining secondary maxima in the diffraction pattern due to single slit is:
A) $a\sin \theta = \dfrac{{n\lambda }}{2}$
B) $a\sin \theta = \dfrac{{(2n - 1)\lambda }}{2}$
C) $a\sin \theta = n\lambda $
D) $a\sin \theta = (2n - 1)\lambda $
Answer
122.1k+ views
Hint: Diffraction of light is the property of light bending around the corners such that it spreads out and illuminates areas. Diffraction is really hard to distinguish from interference as both occur simultaneously.
Complete answer:
The diffraction from a single slit gives a characteristics pattern. Diffusion effects are usually noticeable with the slit with size not very much larger than the wavelength.

The above diagram represents a laser illuminating a single slit and a double slit and the resultant pattern is projected on the screen. The pattern is maximum at centre as the light travels from an equal distance from the slit .The central pattern is broad and is equally spaced from either side with weaker maxima.
For calculating first order minima, assuming a slit width a and divide it in two equal halves .From Huygens principle and considering parallel rays from the both sides at angle to the axis of symmetry.
The ray that will come from a distance of a/2 from below will travel extra distance $\left( {a\sin \dfrac{\theta }{2}} \right)$ when the distance is half the wavelength then $a\sin \theta = \lambda .$
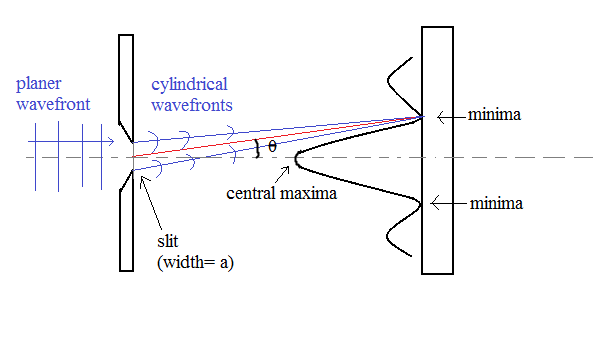 For maxima, the distance between two nth second maxima with central maxima is calculated
For maxima, the distance between two nth second maxima with central maxima is calculated
as: ${x_n} = D\theta = \dfrac{{(2n + 1)}}{{2b}} = \dfrac{{(2n + 1)\lambda f}}{{2b}}$
Where \[b = a\] (width of the slit)
Therefore the diffraction pattern due to single slit for secondary maxima is:
$a\sin \theta = (2n - 1)\dfrac{\lambda }{2}$
Where, $n = 2,3,4,..$
Hence option (B) is the correct option.
Note: Diffractions are only observed with waves travelling in two dimension or three dimension. Diffraction is interference phenomenon where interference of an infinite number of waves emitted by a continuous distribution of source points in two or three dimensions.
Complete answer:
The diffraction from a single slit gives a characteristics pattern. Diffusion effects are usually noticeable with the slit with size not very much larger than the wavelength.

The above diagram represents a laser illuminating a single slit and a double slit and the resultant pattern is projected on the screen. The pattern is maximum at centre as the light travels from an equal distance from the slit .The central pattern is broad and is equally spaced from either side with weaker maxima.
For calculating first order minima, assuming a slit width a and divide it in two equal halves .From Huygens principle and considering parallel rays from the both sides at angle to the axis of symmetry.
The ray that will come from a distance of a/2 from below will travel extra distance $\left( {a\sin \dfrac{\theta }{2}} \right)$ when the distance is half the wavelength then $a\sin \theta = \lambda .$
 For maxima, the distance between two nth second maxima with central maxima is calculated
For maxima, the distance between two nth second maxima with central maxima is calculated as: ${x_n} = D\theta = \dfrac{{(2n + 1)}}{{2b}} = \dfrac{{(2n + 1)\lambda f}}{{2b}}$
Where \[b = a\] (width of the slit)
Therefore the diffraction pattern due to single slit for secondary maxima is:
$a\sin \theta = (2n - 1)\dfrac{\lambda }{2}$
Where, $n = 2,3,4,..$
Hence option (B) is the correct option.
Note: Diffractions are only observed with waves travelling in two dimension or three dimension. Diffraction is interference phenomenon where interference of an infinite number of waves emitted by a continuous distribution of source points in two or three dimensions.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Mains 2025: Check Important Dates, Syllabus, Exam Pattern, Fee and Updates

JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Chemistry Exam Pattern 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Electric field due to uniformly charged sphere class 12 physics JEE_Main




