Question

The cost of 2 kg apples and 1 kg of grapes on a day was found to be Rs. 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs. 300. Represent the situation algebraically and geometrically.

Answer 1

Hint: Be clear that the two cases given in the question are completely different and will give two equations which are independent of each other. While you will represent them geometrically you will get two different lines on the Cartesian plane.

Complete step-by-step solution -
Before starting with the solution, let us discuss the significance of linear equations in two variables. Linear equations in two variables represent the equation of a line on the Cartesian plane.
Now we will move to the solution to the given question. First, let us solve for the initial case when the cost of 2 kg apples and 1 kg of grapes was Rs. 160. We let the price of the apples be Rs. x per kg and the price of the grapes be Rs. y per kg. Using this data, we can mathematically represent the case as:
2x + y = 160
Now, as this is a linear equation, it represents a line. In order to represent this in a Cartesian plane, we convert the equation of line to the Cartesian form. On doing so, we get
2x + y = 160
\[\Rightarrow \dfrac{x}{80}\text{ }+\text{ }\dfrac{y}{160}\text{ }=\text{ }1\]
Therefore, the x-intercept of the line is 80, and the y-intercept is 160. So, the line will meet the x-axis and the y-axis at (80,0) and (0,160). This can be geometrically represented as:

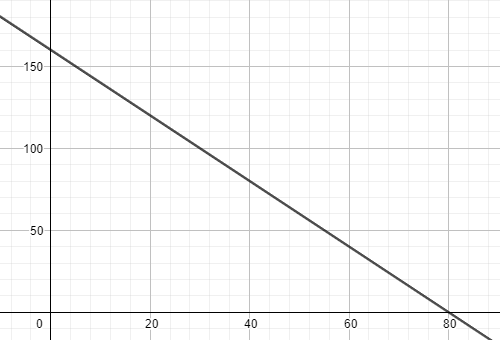
Similarly, let us solve for the final case when the cost of 4 kg apples, and 2 kg of grapes was Rs. 300. We let the price of the apples be Rs. x per kg and the price of the grapes be Rs. y per kg. Using this data, we can mathematically represent the case as:
4x + 2y = 300
Now, as this is a linear equation, it represents a line. In order to represent this in a Cartesian plane, we convert the equation of line to the Cartesian form. On doing so, we get
4x + 2y = 300
\[\Rightarrow \dfrac{x}{75}\text{ }+\text{ }\dfrac{y}{150}\text{ }=\text{ }1\]
Therefore, the x-intercept of the line is 75, and the y-intercept is 150. So, the line will meet the x-axis and the y-axis at (75,0) and (0,150). This can be geometrically represented as:

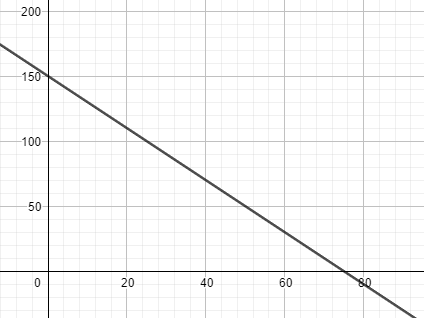
Note: Be careful with the signs and calculations as in such questions, the possibility of making a mistake is either of the sign or a calculation error. Also, we should be clear that a solution can represent different geometries when represented in planes with different dimensions, and all the points lying on these geometries would represent a solution to the linear equation. For example: when the solution of the above equation is represented on a number line, i.e., a single dimensioned plane, the geometry formed is just a point while on the Cartesian plane, it is represented by a straight line. Further, if we extend it to a 3-D plane, we will find the same solution will represent a plane.