Question

The current gain of a common emitter transistor circuit shown in figure is $120$. Draw the dc load line and mark the Q point in it. (${V_{BE}}$ to be ignored).

Answer 1

Hint: The way to solve these types of questions are using the standard formulas of DC Load line and Voltage Divider Bias formulas. We have been given the value of $\beta = {\text{ 120}}$ . ${{\text{V}}_{cc}} = {\text{ 25V}}$.Now we have to find the Q point using the formula of ${V_{cc}}{\text{ = }}{V_{ce}}{\text{ + }}{{\text{i}}_c}{{\text{R}}_c}$ and ${V_{ce}} = {\text{ }}{V_{cc}} - {{\text{i}}_c}{{\text{R}}_c}$ . We have all the required values given. Whenever not given, assume that ${V_{be}} = 0.7V$ .

Complete step by step answer:
We know that by the formula of voltage divider Bias:
${V_{bb}} - {\text{ }}{i_b}{R_b} - {V_{be}} = 0 - - - - (1)$
Thus, we can get base current from the equation:
${i_b} = \dfrac{{{V_{bb}} - {V_{be}}}}{{{R_b}}}$
Thus, ${i_b} = \dfrac{{25 - 0.7}}{{{{10}^6}}}$
Now, we know that collector current is related to base current by the formula:
${i_c} = {\text{ }}\beta {i_b}$
hence, ${i_c} = {\text{ 120(}}\dfrac{{25 - 0.7}}{{{{10}^6}}})$
Now by using ${V_{cc}}{\text{ = }}{V_{ce}}{\text{ + }}{{\text{i}}_c}{{\text{R}}_c}{\text{ }}$
${V_{ce}} = {\text{ }}{V_{cc}} - {{\text{i}}_c}{{\text{R}}_c}$
Thus ${V_{ce}} = 25 - ({{\text{i}}_c} \times 5 \times {10^3})$.

Now we can easily plot the Q point by using the values of ${V_{ce}}$ and ${i_c}$ , by plotting a graph along them , considering \[\]${V_{ce}}$ as the X axis and ${i_c}$ as the Y axis. We have to consider ${i_c}$ is zero when we have to calculate the value of ${V_{ce}}$ and the value of ${V_{ce}}$ as zero when we have to find the value of ${i_c}$ . Now we will get a line passing through the first two points and now according to the given value of \[{V_{be}}\] , we have to point to the Q point.

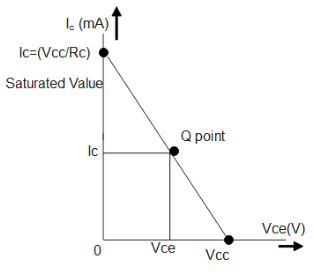
Note: These sums come only with this one type of questions, just find the variables needed and graph it, if the value of \[{V_{be}}\] is given, draw a line according to it, or else take it as $0.7$ (remember) and move ahead. The point of intersection is very easy to find as almost all values are given in the question. Note that you remember how collector current, base current, collector emf, base emf are all interrelated to each other.