Question

The curved surface of a cylinder is developed from a square whose diagonal is $2\sqrt{2}cm$. Find the area of the base of the cylinder in square centimetres
[a] $3\pi $
[b] $\dfrac{1}{\pi }$
[c] $\pi $
[d] $6\pi $

Answer 1

Hint: Assume that the length of a side of the square is a. Use the fact that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Hence find the length of diagonal in terms of a. Equate this expression to the given length of the diagonal and hence form an equation in a. Solve for a and hence find the side length of the square. Use the fact that when the square is converted to the cylinder, one side will become the circumference of the base and the other side will be the height of the cylinder. Hence find the radius of the cylinder. Hence find the area of the base of the cylinder.
Complete step by step answer:

Let the length of a side of the square ABCD be a.
We know that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is known as Pythagoras theorem.
Now, in triangle ABC, we have by Pythagoras theorem
$\begin{align}
  & A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \\
 & \Rightarrow A{{C}^{2}}={{a}^{2}}+{{a}^{2}} \\
 & \Rightarrow A{{C}^{2}}=2{{a}^{2}} \\
\end{align}$
But given that $AC=2\sqrt{2}$
Hence, we have
$\begin{align}
  & 2{{a}^{2}}={{\left( 2\sqrt{2} \right)}^{2}} \\
 & \Rightarrow 2{{a}^{2}}=8 \\
\end{align}$
Dividing both sides by 2, we get
${{a}^{2}}=4$
Hence, we have
a = 2

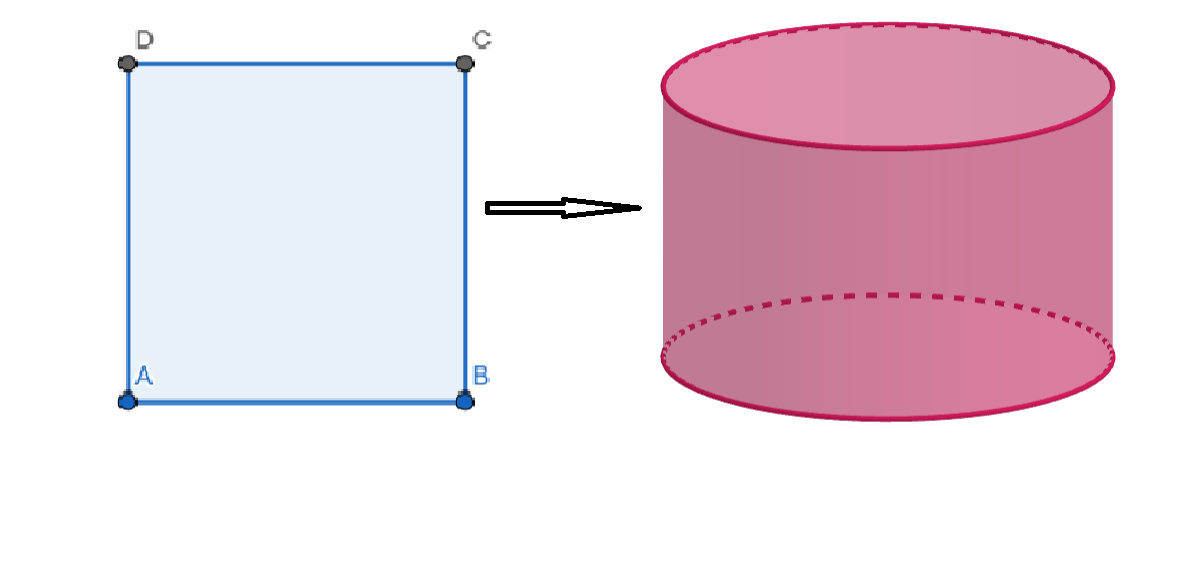
Now, when ABCD is converted to a cylinder, we have AB will become the circumference of the base and BC becomes the height of the cylinder.
Let r be the radius of the base of the cylinder.
Hence, we have the circumference of the base $=2\pi r$
Since the circumference of the base is equal to AB, we have
$2\pi r=2$
Dividing both sides by $2\pi $, we get
$r=\dfrac{1}{\pi }$
Now, we have area of the base of the cylinder $=\pi {{r}^{2}}=\pi {{\left( \dfrac{1}{\pi } \right)}^{2}}=\dfrac{1}{\pi }c{{m}^{2}}$
Hence option [b] is correct.
Note: In these types of questions, we need to visualise what happens to the sides of the square when converted in the cylinder. Students can try by cutting a square piece of paper and verifying the above argument.
Some students make a mistake by finding the curved surface area of the cylinder(as it is mentioned in the question at the beginning and they hastefully do not read the whole question) instead of the area of the base and end up with incorrect results. It is important to read the question carefully.