
The cyclotron frequency of an electrons gyrating in a magnetic field of $1\,T$ is approximately:
A) $28\,MHz$
B) $280\,MHz$
C) $2.8\,MHz$
D) $28\,GHz$
Answer
123.6k+ views
Hint: To find the value of the frequency of the cyclotron of an electron, use the formula below and substitute the value of the magnetic induction, charge and mass of the electron in it , the obtained result provides the answer for the frequency of cyclotron.
Useful formula:
The formula of the frequency of the cyclotron is given by
$\nu = \dfrac{{qB}}{{2\pi m}}$
Where $\nu $ is the frequency of the cyclotron, $q$ is the charge of the electron, $B$ is the magnetic field and $m$ is the mass.
Complete step by step solution:
It is given that the
Magnetic field that is used in the cyclotron, $B = 1T$
Use the formula of the frequency of the cyclotron,
$\nu = \dfrac{{qB}}{{2\pi m}}$
Substitute the values of the charge $q = 1.6 \times {10^{ - 19}}$ , the magnetic induction from the given, $m = 9.1 \times {10^{ - 31}}$ as the mass of the electron in the above used formula.
$\nu = \dfrac{{1.6 \times {{10}^{ - 19}} \times 1}}{{2 \times 3.14 \times 9.1 \times {{10}^{ - 31}}}}$
Simplifying the above equation, we get
$\nu = \dfrac{{0.8 \times {{10}^{12}}}}{{3.14 \times 9.1}}$
By the further simplification of the above step,
$\nu = 28 \times {10^9}\,Hz$
It is known that the $1\,GHz = {10^9}\,Hz$ , substituting this in the above step
$\nu = 28 \times {10^9}\,GHz$
Hence the cyclotron frequency of the electron is obtained as $\nu = 28\,GHz$. It is not $28\,MHz$ since $1\,MHz = {10^6}\,HZ$ .
Thus the option (D) is correct.
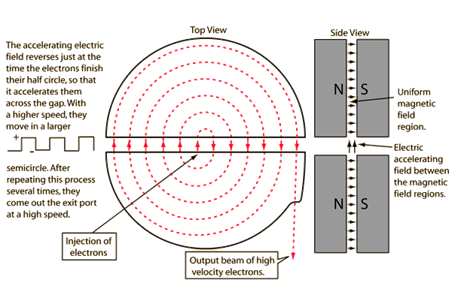
Note: The cyclotron frequency mainly depends upon the specific charge and the magnetic induction. The specific charge is calculated by dividing the charge of the particle and the mass of it. The use of the cyclotron is to produce the radioactive isotopes which are used in the process of the imaging procedures.
Useful formula:
The formula of the frequency of the cyclotron is given by
$\nu = \dfrac{{qB}}{{2\pi m}}$
Where $\nu $ is the frequency of the cyclotron, $q$ is the charge of the electron, $B$ is the magnetic field and $m$ is the mass.
Complete step by step solution:
It is given that the
Magnetic field that is used in the cyclotron, $B = 1T$
Use the formula of the frequency of the cyclotron,

$\nu = \dfrac{{qB}}{{2\pi m}}$
Substitute the values of the charge $q = 1.6 \times {10^{ - 19}}$ , the magnetic induction from the given, $m = 9.1 \times {10^{ - 31}}$ as the mass of the electron in the above used formula.
$\nu = \dfrac{{1.6 \times {{10}^{ - 19}} \times 1}}{{2 \times 3.14 \times 9.1 \times {{10}^{ - 31}}}}$
Simplifying the above equation, we get
$\nu = \dfrac{{0.8 \times {{10}^{12}}}}{{3.14 \times 9.1}}$
By the further simplification of the above step,
$\nu = 28 \times {10^9}\,Hz$
It is known that the $1\,GHz = {10^9}\,Hz$ , substituting this in the above step
$\nu = 28 \times {10^9}\,GHz$
Hence the cyclotron frequency of the electron is obtained as $\nu = 28\,GHz$. It is not $28\,MHz$ since $1\,MHz = {10^6}\,HZ$ .
Thus the option (D) is correct.
Note: The cyclotron frequency mainly depends upon the specific charge and the magnetic induction. The specific charge is calculated by dividing the charge of the particle and the mass of it. The use of the cyclotron is to produce the radioactive isotopes which are used in the process of the imaging procedures.
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

JEE Main Login 2045: Step-by-Step Instructions and Details

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Physics Average Value and RMS Value JEE Main 2025

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!




