
The density of
a)253 pm
b)344 pm
c)546 pm
d)273 pm
Answer
409.5k+ views
Hint: Crystal structure is a description of the orderly organisation of atoms, ions, or molecules in a crystalline substance used in crystallography. The inherent nature of the component particles results in symmetric patterns that recur along the major directions of three-dimensional space in matter, forming ordered structures.
Complete answer:
Calcium fluoride (
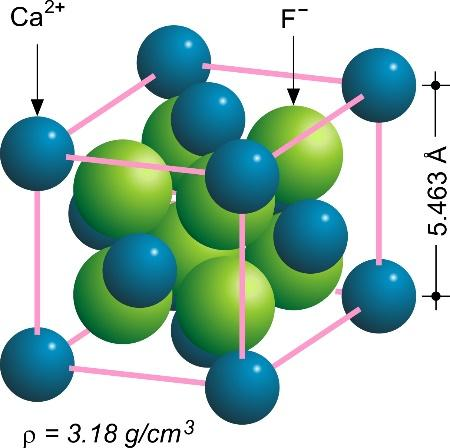
The unit cell of the structure is the smallest group of particles in the substance that makes up this repeating pattern. The symmetry and structure of the whole crystal are perfectly reflected in the unit cell, which is built up by recurrent translation of the unit cell along its major axes. The nodes of the Bravais lattice are defined by the translation vectors.
We know that
D = density
M= mass
V= volume (
For fluorite structure,
Hence option c is correct.
Note:
Knowing the dimensions of the unit cell allows us to calculate the volume of the unit cell. For example, if an edge "a" has a unit cell, the volume of the unit cell may be written as "
Complete answer:
Calcium fluoride (

The unit cell of the structure is the smallest group of particles in the substance that makes up this repeating pattern. The symmetry and structure of the whole crystal are perfectly reflected in the unit cell, which is built up by recurrent translation of the unit cell along its major axes. The nodes of the Bravais lattice are defined by the translation vectors.
We know that
D = density
M= mass
V= volume (
For fluorite structure,
Hence option c is correct.
Note:
Knowing the dimensions of the unit cell allows us to calculate the volume of the unit cell. For example, if an edge "a" has a unit cell, the volume of the unit cell may be written as "
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




