Question

The depth of the pond is 10m. What is the apparent depth for a person looking normally to the water surface? ${\mu}_{\text{water}}=\dfrac{4}{3}$

Answer 1

Hint Real depth is refractive index times apparent depth. Consider the given depth to be the real depth of the pond, multiply it with the refractive index and get the apparent depth of the pond.

Complete step-by-step solution
Let real depth of the pond be x and apparent depth of the pond be y.
From the question we know, the real depth of the pond is \[{\text{10m}}\].
 \[\therefore x = 10m\,\,\, \ldots (1)\]
The relation between real depth, apparent depth and refractive index is given as,
\[refractive{\text{ }}index = \dfrac{{real{\text{ }}depth}}{{apparent{\text{ }}depth}}\,\, \ldots (2)\]
Rearranging equation.(2) gives,
\[apparent{\text{ }}depth = \dfrac{{real{\text{ }}depth}}{{refractive{\text{ }}index}}\]
\[\therefore {\text{y = }}\dfrac{{\text{x}}}{{{{\mu}_{{\text{water}}}}}}\,\,\,{{ \ldots (3)}}\]

Given: \[{{\mu}_{{\text{water}}}}{\text{ = }}\dfrac{{\text{4}}}{{\text{3}}}\,\,\,{{ \ldots (4)}}\]
Now, substituting equation.(1) and equation.(4) in equation.(3)
$y=\dfrac{10}{\dfrac{4}{3}} \\
\Rightarrow y=10 \times \dfrac{3}{4} \\
\Rightarrow y=5 \times \dfrac{3}{2}
$

Therefore, the apparent depth of the pond is \[7.5m.\]

Additional Information
When a ray of light moves from one medium to another, velocity and direction of the ray changes. This change is due to refraction of ray which causes false appearance of depth of the material.

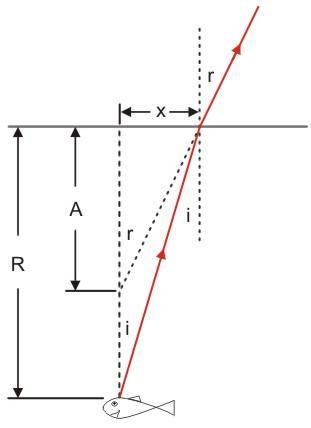
In the figure above, R represents real depth of the fish and A represents apparent depth of the fish.
From the figure we can say,

\[
 \tan i = \dfrac{x}{R} \\
 \tan r = \dfrac{x}{A} \\
\]
From Snell’s Law we know, Refractive Index is given as,
 \[{\mu _{water}} = \dfrac{{\sin r}}{{\sin i}}\]
For small angles, \[\sin i = \tan i\,\]and \[\tan i = \tan r\]
 \[\therefore {{\mu}_{{\text{water}}}}{\text{ = }}\dfrac{{{{\tan r}}}}{{{{\tan i}}}}\]
 \[\therefore \mu = \dfrac{R}{A}\]

Therefore, refractive index is equal to the ratio of real depth and apparent depth.

Note The value of apparent depth is always smaller than the real depth. So, if you get the value of apparent depth greater than the real depth so do check your calculation. Don’t get confused between the real depth and apparent depth.