Question

The diagram below shows a blue cart chasing a yellow cart on a frictionless track. The velocities and masses of the carts are given in the diagram. When the blue cart catches up with the yellow cart, the carts stick together and move as one. What is the momentum of the two-cart system after the collision?

(A) $3.0 \, kg.m/s$
(B) $4.0 \, kg.m/s$
(C) $5.0 \, kg.m/s$
(D) $8.0 \, kg.m/s$
(E) We do not have enough information to determine the momentum of the two-cart system after the collision

Answer 1

Hint:
The concept of the given question is based on the conservation of the linear momentum concept. From the law of conservation of linear momentum, we need to calculate the total momentum of the individual carts before the collision and equate that to the momentum of the combined carts after the collision. So the momentum after the collision will be the same as the momentum before.
$P = mv$
Where $m$ is the mass of an object and $v$ is the velocity of the object.

Complete step by step answer:
The linear momentum of an object is the product of mass and velocity of that object.
So, the formula for calculating the linear momentum is given as,
$P = mv$
In the given case, there are two objects and both are moving along the same direction. So we will consider the initial velocity of the objects to be denoted by “u”. So, we can extend the formula as follows,
$P = {m_1}{u_1} + {m_2}{u_2}$
As the values of the initial condition of both the carts are given, so, we will make use of those values from the question to carry out the calculation.
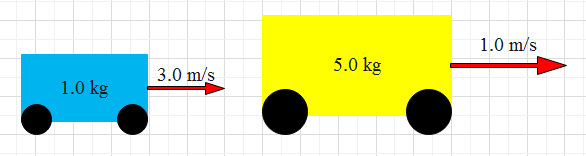
From the diagram, it’s clear that the mass and the velocity of the blue cart is 1 kg and $3{m \mathord{\left/
 {{m s}} \right.} s}$ respectively and the mass and the velocity of the yellow cart is 5 kg and $1{m \mathord{\left/
 {{m s}} \right.} s}$ respectively.
Substituting these values in the above equation we get,
$P = \left( {1 \times 3} \right) + \left( {5 \times 1} \right)$
On calculation this gives a value as,
$P = 8 \, kg.m/s$
Therefore, the momentum of the system before the collision is, ${P_i} = 88{{(kg)(m)} \mathord{\left/
 {\vphantom {{(kg)(m)} s}} \right.} s}$
According to the conservation of linear momentum, the total momentum of the system before the collision will be equal to the total momentum of the system after the collision.
So, we have,
${P_f} = {P_i}$
Now, substituting the value of the initial momentum,
${P_f} = 8\, kg.m/s$
$\therefore $ The momentum of the two-cart system after the collision is $8\, kg.m/s$, thus, option (D) is correct.

Note:
The momentum of a body is the product of the mass of the body and the velocity of that body. The conservation of linear momentum is a property that is exhibited by a body in which the momentum of the body always remains constant in the case when the net external force that is acting on the body is zero.