Question

The diagram below shows a toy airplane from above flying around in a circular path at a constant speed in the direction indicated by the arrows.

Which of the following tables correctly describes the points at which the plane's velocity is south and at which its acceleration is south?
A) Point 4 - Point 2
B) Point 3 - Point 2
C) Point 1 - Point 3
D) Point 2 - Point 4
E) Point 2- Point 4

Answer 1

Hint: In a circular motion, the velocity of the object is always tangential to the motion of the object. And the acceleration of an object in circular motion is the resultant of radial and angular acceleration.

Complete step by step solution:
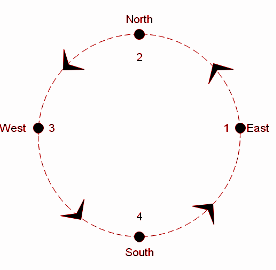
When a particle moves in a circular motion, its linear velocity is always tangential to the direction of its motion at that given point in the circular path. It is clear from the figure that when the toy airplane is at point 3, the tangent to its direction of motion will be downwards as the plane is moving in an anti-clockwise direction. While point 4 will have velocity in the east direction, point 1 in the North, and point 2 in the West.
On the other hand, the acceleration of the toy in a circular motion will be due to the resultant of the linear acceleration and the angular acceleration. But since the toy airplane is moving with constant velocity, it will have zero linear acceleration. The angular acceleration will be due to the centripetal force that acts on the airplane that acts in the inwards direction i.e. towards the center of the trajectory. So, the toy plane’s acceleration will be in the South direction, when it is in the North position i.e. point 2
So, the velocity will be downwards when the airplane is at point 3 and the acceleration will be downwards when it is at point 2 which corresponds to option (B).

Note:
In a circular motion, the velocity of the object is always tangential while the acceleration, in this case, is always towards the center i.e. perpendicular to the tangential direction which is why the particle travels in a circular trajectory. We must be very careful about taking the direction of the circular motion into account. If the trajectory had been in the clockwise direction, the point having a velocity in the downwards direction would be point 1 however the acceleration in the downwards direction would still be at point 2 since the acceleration of the plane is towards the center regardless of the direction of motion.