Question

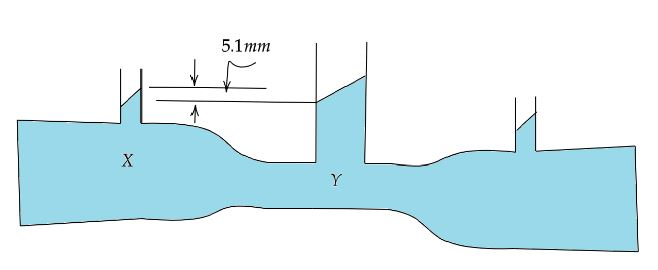
The diagram shows a venturimeter through which water is flowing. The speed of water $X$ is $2\,cm{s^{ - 1}}$. The speed of water at $Y$ ( taking $g = 10\,m{s^2}$ ) is

A. $23\,cm{s^{ - 1}}$
B. $32\,cm{s^{ - 1}}$
C. $101\,cm{s^{ - 1}}$
D. $1024\,cm{s^{ - 1}}$

Answer 1

Hint:Here we have to use the formula of the venturimeter. The formula shows the pressure difference between $X$ that is before narrowing of the pipe and $Y$ that is after narrowing of the pipe. After that using the pressure difference formula of fluid we can solve the equation to find the value of speed of water at $Y$.

Complete step by step answer:
As per the problem we have a venturimeter through which water is flowing. The speed of water X is $2\,cm{s^{ - 1}}$. Now we need to calculate the speed of water at Y.
We know venture effect is represented as,
$p_x - p_y = \dfrac{\rho }{2}\left( {v{y^2} - {v_x}^2} \right) \ldots \ldots \left( 1 \right)$
Where, Pressure at position X before the narrowing of the pipe is $px$, Pressure at position Y after the narrowing of the pipe is $p_y$, Density of fluid travelling in the pipe is $\rho $, Velocity of the fluid at position Y is $v_y$ and Velocity of the fluid at position X is $v_x$.

The pressure difference is also represented as,
$p_x - p_y = \Delta h\rho g \ldots \ldots \left( 2 \right)$
Where,
$\Delta h$ is the change in height due to change in before and after narrowing of the pipe.
Now equation equation $\left( 1 \right)$ and $\left( 2 \right)$ we will get,
$\dfrac{\rho }{2}\left( {{v_y}^2 - v_{x^2}} \right) = \Delta h\rho g$
Now cancelling the common terms we will get,
$\dfrac{1}{2}\left( {{v_y}^2 - {v_x}^2} \right) = \Delta hg$

We know,
$\Delta h = 5.1mm = 0.51cm$
$\Rightarrow v_x = 2cm{s^{ - 1}}$
$\Rightarrow g = 10\,m{s^{ - 1}} = 1000\,cm{s^{ - 1}}$
Now putting the given values in the above equation we will get,
$\dfrac{1}{2}\left( {{v_y}^2 - {2^2}} \right) = 0.51 \times 1000$
Now on rearranging and solving further solving we will get,
${v_y}^2 = \left( {510 \times 2} \right) + 2 = 1024$
Hence we can say the speed of water at Y is $32\,cm{s^{ - 1}}$.

Therefore the correct option is $\left( B \right)$.

Note:Here we converted all the units of length in centimeter as our option is given in centimeter. Remember that a venturimeter is a device which is used to measure the rate of flow of fluid flowing through a pipe. The principle of venturimeter is that when a fluid flows through it, it’s acceleration in the convergent section and decelerates in the divergent section which results in drop in static pressure.