Question

The dimension of a solid iron cuboid is 4.4 m X 2.6 m X 1.0 m. It is melted and reacts into a hollow cylindrical pipe of 30cm inner radius and thickness 5cm. Find the length of the pipe.

Answer 1

Hint: Let us find the volume of the solid iron cuboid because it is melted and when we are given the case of melting then our initial and final volume should be the same.

Complete step-by-step answer:

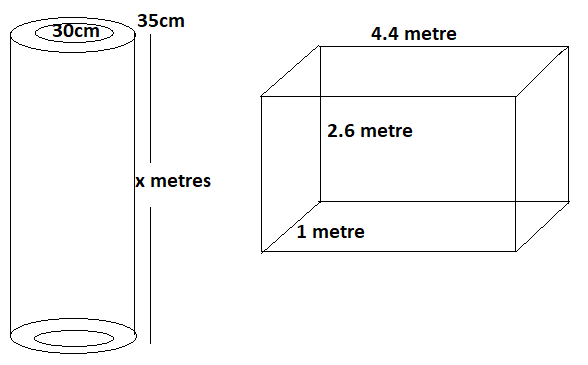
As we know that the volume of the cuboid is length*breadth*height. So, the length of the given cuboid will be (4.4 * 2.6 * 1.0) \[{{\text{m}}^{\text{3}}}\] = 11.44 \[{{\text{m}}^{\text{3}}}\].
So, the volume of the material used in making a hollow cylindrical pipe will be 11.44 \[{{\text{m}}^{\text{3}}}\].
Let the length of the pipe be x metres.
So, as we know that the volume of a hollow cylinder is equal to the volume of the outermost cylinder minus the volume of the innermost cylinder.
And the volume of any cylinder having radius r and length h is \[\pi {{\text{r}}^{\text{2}}}{\text{h}}\].
Inner radius of the pipe is given as 30cm = 0.3 metre.
The thickness of the pipe is 5cm.
So, the outer radius of the pipe will be (30 + 5)cm = 35 cm = 0.35 metre.
And the outer volume of the pipe will be \[\left( {\pi {{\left( {{\text{0}}{\text{.35}}} \right)}^{\text{2}}}{\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\] = \[\left( {{\text{0}}{\text{.1225}}\pi {\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\].
And the inner volume of the pipe will be \[\left( {\pi {{\left( {{\text{0}}{\text{.30}}} \right)}^{\text{2}}}{\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\] = \[\left( {{\text{0}}{\text{.0900}}\pi {\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\].
So, the volume of hollow cylindrical pipe will be \[\left( {{\text{0}}{\text{.1225}}\pi {\text{x - 0}}{\text{.0900}}\pi {\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\] = \[\left( {{\text{0}}{\text{.0325}}\pi {\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\].
As we know that the solid cuboid should be equal to the volume of hollow cylindrical pipe.
So, 11.44 \[{{\text{m}}^{\text{3}}}\] = \[\left( {{\text{0}}{\text{.0325}}\pi {\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\]
11.44 \[{{\text{m}}^{\text{3}}}\] = \[\left( {{\text{0}}{\text{.0325}}\pi {\text{x}}} \right){\text{ }}{{\text{m}}^{\text{3}}}\]
So, x = \[\dfrac{{{\text{11}}{\text{.44 }}}}{{{\text{0}}{\text{.0325 * 3}}{\text{.14}}}}\] = 112.1 m
x = 112.1 metres
Hence, the length of the hollow cylindrical pipe will be 112.1 metres.

Note: Whenever we come up with this type of problem then first, we will find the volume of cuboid using formula (length * breadth * height) and then we will find the volume of hollow cylinder using formula \[\left( {\pi {{\text{R}}^{\text{2}}}{\text{h - }}\pi {{\text{r}}^{\text{2}}}{\text{h}}} \right)\], where R is the outermost radius of pipe, r is the innermost radius of the pipe and h is the length of the pipe. After that we will equal both volumes to get the required length of the hollow pipe.