Question

The dimensions of the floor of a rectangular hall are \[4m \times 3m\]. The tiles floor of the hall is to be tiled with regular tiles with \[8cm \times 6cm\] dimensions without breaking tiles to smaller size. The number of tiles required:
A. 4800
B. 2600
C. 2500
D. 2400

Answer 1

Hint: At first, we will find the area of the floor of the hall and the area of each tile. Then, take the number of tiles as n to be tiled. Then, write it as, \[n \times {\text{area of tile is equal to area of the floor}}\].

Complete step by step solution:
In the question, the dimensions of the floor of a rectangular hall are 4m by 3m. Now, we are told that the floor of the hall will be filled with tiles of rectangular shape with dimension 8cm by 6cm without breaking into smaller sizes. Let us consider the figure below,

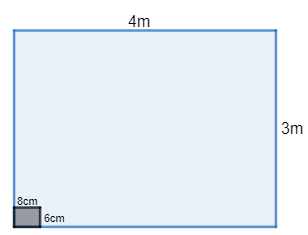
So, we know, the dimension of the floor of the rectangular hall is 4m by 3m.
Now, as we know that, 1m can be measured as 100cm. So, we can say that the dimension of the rectangular floor is \[4 \times 100cm \Rightarrow 400cm\] by \[3 \times 100cm \Rightarrow 300cm.\] So, the dimensions are 400cm by 300cm.
We will find the area of the floor using the formula, area equals the product of length and breadth which is 400cm and 300cm respectively.
So, the area is \[400cm \times 300cm{\rm{ }} \Rightarrow {\rm{120000c}}{{\rm{m}}^{\rm{2}}}\]
Here, the area of floor is \[120000c{m^2}\]
Now, we will find the area of each tile whose given dimensions are 8cm by 6cm.
The area of each tile is the product of length and breadth which is 8cm and 6cm respectively. So, the area of the tile is \[8cm \times 6cm{\rm{ }} \Rightarrow {\rm{48c}}{{\rm{m}}^{\rm{2}}}\]
Let, the total number of tiles to be placed on the floor is n. So, we can write that the total area covered by n tiles would be \[n \times 48{\rm{ }} \Rightarrow {\rm{48n}}{\rm{.}}\]The total area of floor is 120000. So, we can say that,
\[\begin{array}{l}48n = 120000\\ \Rightarrow {\text{the value of n is }}\dfrac{{120000}}{{48}}{\rm{ }} \Rightarrow {\rm{2500}}{\rm{.}}\end{array}\]
Hence, the total number of tiles is 2500.
Therefore, the correct option is C.

Note: Generally, students do not check that the dimensions are different and thus, start doing operations on it, which make their answer wrong. Thus, students should first check the units of measurement first and then convert it to a single unit before proceeding.