Question

The distance between two point sources of light is 24cm. Find out where you would place a converging lens of focal length $$9cm$$, so that the images of both the sources are formed at the same point.

Answer 1

Hint: For lens the distance of the image formed from the lens is given by $${\displaystyle \frac{1}{v}}-{\displaystyle \frac{1}{u}}={\displaystyle \frac{1}{f}}$$ where $$u,v$$ and $f$ are a distance of the object, a distance of image, and the focal length respectively.

The focal length is the distance from the center of the lens to the principal foci or the focal points of the lens. For a converging lens, the best example is a convex lens. The focal length is positive and the interval at which a beam of collimated light will be focused on a single spot.

Complete step by step solution:

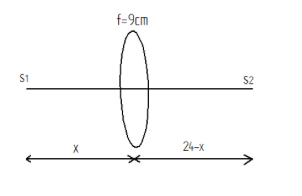
$S_1$we have to take the equation as
${\displaystyle \frac{1}{v_1}}-{\displaystyle \frac{1}{-x}}={\displaystyle \frac{1}{9}}$
Then the equation becomes
${\displaystyle \frac{1}{v_1}}+{\displaystyle \frac{1}{x}}={\displaystyle \frac{1}{9}}$
Now we want the value of ${\displaystyle \frac{1}{v_1}}$ so take it outside
${\displaystyle \frac{1}{v_1}}={\displaystyle \frac{1}{9}}-{\displaystyle \frac{1}{x}}.........(1)$
Now for$S_2$we have to take the equation as
${\displaystyle \frac{1}{v_2}}-{\displaystyle \frac{1}{-(24-x)}}={\displaystyle \frac{1}{9}}$
Then the equation becomes
${\displaystyle \frac{1}{v_2}}+{\displaystyle \frac{1}{(24-x)}}={\displaystyle \frac{1}{9}}$
Now we want the value of ${\displaystyle \frac{1}{v_2}}$ so take it outside
${\displaystyle \frac{1}{v_2}}={\displaystyle \frac{1}{9}}-{\displaystyle \frac{1}{(24-x)}}$
Now Since, the sign convention for $S_1$ and $$S_2$$is just opposite. Hence, we should take
$v_1=-v_2$
Then the equation becomes
$\Rightarrow {\displaystyle \frac{1}{v_1}}=-{\displaystyle \frac{1}{v_2}}$
Therefore now substitute the values so we get
${\displaystyle \frac{1}{9}}-{\displaystyle \frac{1}{x}}={\displaystyle \frac{1}{24-x}}-{\displaystyle \frac{1}{9}}$
Solving this equation, we get $$x=6cm$$. Therefore, the lens should be kept at a distance of $$6cm$$ from either of the objects.

Note: A converging lens is defined as a lens that converges rays of the light that are moving parallel to the principal axis. The fact that a double convex lens is thicker across its middle is an indicator that it will converge rays of light that move parallel to its principal axis.