Question

The edge length of the unit cell of a body-centered cubic (bcc) crystal is 352 pm. Calculate the radius of the atom.

Answer 1

Hint: You should know that in body-centered-cubic crystal the length of body diagonal is equal to the diameter of two atoms. Now try to find the relation between them and calculate the final answer.

Complete Solution :
There are many types of unit cells in the like simple unit cell, face-centered cubic cell, body-centered cubic cell. In a simple unit cell, all the atoms are only at the corner of the cube. When the atoms are present at the center of the unit cell and at the center of the face are body centered and face centered unit cell respectively.
Let’s look at the structure of body-centered cubic:

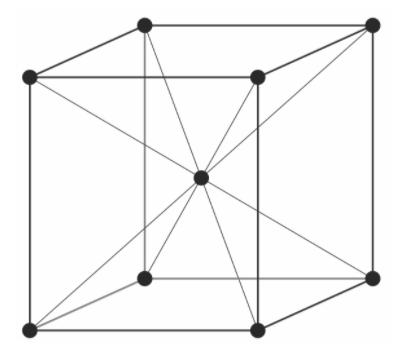
Suppose we have a cube with edge length a, so its body diagonal will be equal to 3a.
In the body-centered cubic lattice, a total 4 radius (one complete atom and two half atoms) participate at the body diagonal.
So, we can write it as,
Length of body diagonal = radius of 4 atom
3a = 4r
1.732 x 352 pm = 4r
r = 1.732 x 88 pm
r = 152.42 pm
Therefore, we can conclude that the radius of the atom with the edge length of the unit cell of a body-centered cubic (bcc) crystal 352 pm, will be equal to 152.42 pm.

Note: As we can see there are 8 atoms at the corners of the lattice, the contribution of those is 1/8, which makes the total contribution equal to one. One atom is at the center, the contribution of this atom will be one. So, we can say the total atom in a body-centered cubic lattice is equal to two. In the bcc structures, the spheres fill 68 % of the volume.