Question

The E-isomer is shown by:

A.

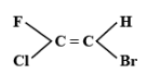
B.

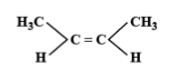
C.

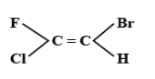
D.

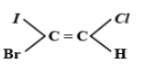
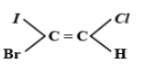
Answer 1

Hint: To answer this question, recall the concept of geometrical isomerism. Geometrical isomerism is defined as the type of stereoisomerism having the same molecular formula and same structure but differ in the relative arrangement of atoms. E isomer is analogous to the trans isomer and Z isomer is analogous to cis isomer.

Complete step by step answer:
We know that isomers are defined as the molecules with the same molecular formula but possess a different arrangement of the atoms in space or different connectivity of atoms. The phenomenon in which the molecules that form the isomers are connected differently is known as structural isomerism. The phenomenon in which the connectivity of atoms is the same in isomers but a different spatial arrangement is a stereoisomerism.
The E-Z isomerism is a type of geometrical isomerism when all the four groups attached are different. In case the two groups with the higher priorities i.e. higher atomic number are on the same side of the double bond, then that molecule is termed as Z- isomer. So, the IUPAC name of that compound will be (Z)-name of the compound. The symbol Z denotes together and is derived from the German word zusammen. In the second case if the two groups with the higher priorities i.e. higher atomic number are attached on opposite sides of the double bond, then this isomer is called (E)- isomer. E means opposite and is derived from the German word entgegen.
We can write the isomers for the given compounds as:

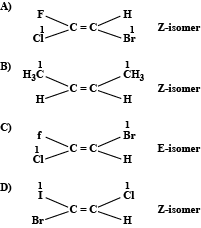
Hence option C is correct.

Note:
Geometric isomerism is one of the forms of stereoisomerism. The key point in geometrical isomers is the restricted rotation of a bond present somewhere in a molecule. At the most basic level of organic chemistry, carbon-carbon double bond is one of the examples leading to a restricted rotation.