
The electric field at A due to an electric dipole, is perpendicular to the dipole moment vector $\overrightarrow P $, the angle θ is:

A) $0$
B) $90^\circ$
C) ${tan}^{-1}(\dfrac{1}{2})$
D) ${tan}^{-1}(\sqrt 2)$
Answer
140.7k+ views
Hint: An electric dipole is defined as a couple of opposite charges $q$ and $ - q$ separated by a distance $d$. By default, the direction of electric dipoles in space is always from negative charge $ - q$to positive charge $q$. The midpoint $q$ and $ - q$is called the center of the dipole. There is always an electric field accompanying a dipole and it is in two perpendicular directions along with it.
Complete step by step solution:
It is given in the question that suppose $\vec P$ is an electric dipole with direction as shown in the figure now consider an axis inclined at an angle $\theta $ (refer figure) (the image has been rotated for understanding purpose)
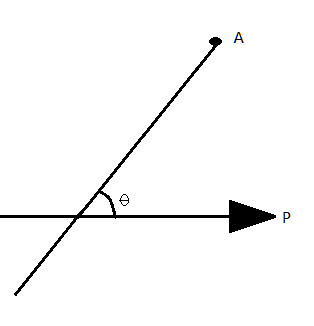
The direction on the net electric field is given perpendicular to the dipole.
So, for this, we need to find out, so we need to find the angle $\theta $ on the dipole up to which the axis is inclined.
So for this, we bifurcate the dipole $\vec P$ and take its component along the inclined axis and the axis perpendicular to it (refer figure)
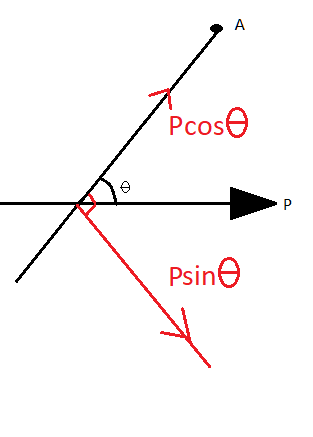
So the component along the inclined axis will be $\vec P\cos \theta $ and the other component will be $\vec P\sin \theta $.
Now for our ease, we will treat the component $\vec P\cos \theta $ as a single dipole.
Now,
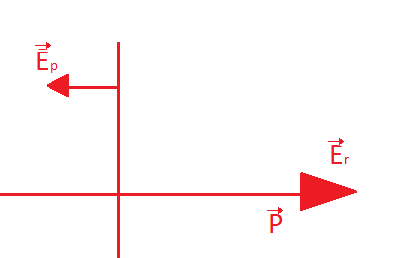
As we know if $\vec X$ be a dipole along the x-axis so electric field along that axis at a distance $r$ due to the dipole is given as:
${\vec E_r} = \dfrac{{2k\vec X}}{{{r^3}}}$
and its direction will be the same as the dipole direction.
Due to this as we know there will also be an electrical field in the equatorial plane and perpendicular to it will be given by
${\vec E_p} = \dfrac{{k\vec X}}{{{r^3}}}$
and its direction will be opposite to that of the initial field
See figure
Similarly, the electrical field along the direction of $\vec P\cos \theta $ will be
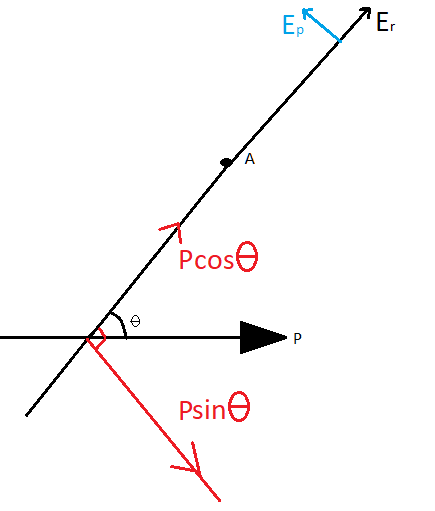
Here the value of $\vec P$ will be $\vec P\cos \theta $
so electrical field will be ${\vec E_r} = \dfrac{{2k\vec P\cos \theta }}{{{r^3}}}$
And now along its equatorial plane at the perpendicular axis, the value of electrical field will be ${\vec E_p} = \dfrac{{k\vec P\sin \theta }}{{{r^3}}}$
Now here the value of $\vec P$ will be $\vec P\sin \theta $ because the field in that direction is caused by the component $\vec P\sin \theta $ of dipole $\vec P$ so it will be in the equatorial plane of the dipole perpendicular to the initial field and opposite direction.
So now the resultant of these two fields will be somewhere between them let it be at an angle $\alpha $.
Now,
Using trigonometry
$
\operatorname{tan} \alpha = \dfrac{{\overrightarrow {{E_p}} }}{{\overrightarrow {{E_r}} }} \\
\therefore \operatorname{tan} \alpha = \dfrac{{\left( {\dfrac{{k\vec P\sin \theta }}{{{r^3}}}} \right)}}{{\left( {\dfrac{{2k\vec P\cos \theta }}{{{r^3}}}} \right)}} \\
\Rightarrow \operatorname{tan} \alpha = \dfrac{{\sin \theta }}{{2\cos \theta }} \\
\Rightarrow \operatorname{tan} \alpha = \dfrac{{\tan \theta }}{2} \\
$
$ \Rightarrow \operatorname{tan} \theta = 2\operatorname{tan} \alpha $___________________(1)
Now as we need to find $\theta $ so we need to eliminate $\alpha $and make in term of $\theta $
So as we can see in the question it is given that the net of the electric field should be perpendicular to the dipole so we extend the resultant line.
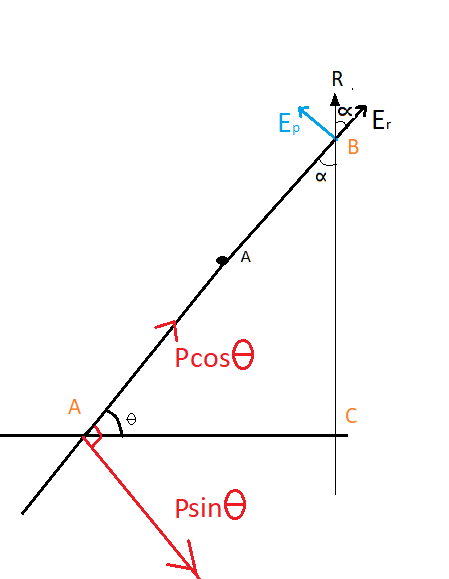
Refer triangle $\vartriangle ABC$ here we can hat the angle $\theta $ will be equal $\angle ABC$ due to the vertically opposite angle
$\vartriangle ABC$ is a right angle triangle so we can say that
$
\theta + \alpha = 90^\circ \\
\theta = 90^\circ - \alpha \\
$
So taking $\operatorname{tan} $ on both sides we get
$\operatorname{tan} \theta = \operatorname{tan} \left( {90 - \alpha } \right)$
Or $\operatorname{tan} \theta = cot\alpha $__________________(2)
The value $cot\alpha $ can be calculated from equation (1)
$
\because \operatorname{tan} \theta = 2\operatorname{tan} \alpha \\
\therefore cot\alpha = \dfrac{2}{{\operatorname{tan} \theta }} \\
$
So, substituting it in the above equation (2)
$
\operatorname{tan} \theta = \dfrac{2}{{\operatorname{tan} \theta }} \\
\Rightarrow {\operatorname{tan} ^2}\theta = 2 \\
\Rightarrow \operatorname{tan} \theta = \sqrt 2 \\
\Rightarrow \theta = {\operatorname{tan} ^{ - 1}}\sqrt 2 \\
$
Final answer is (D), The value of $\theta $ will be ${\operatorname{tan} ^{ - 1}}\sqrt 2 $.
Note: The electric fields accompanying the electric dipole will always be perpendicular to each other. The direction of the electric field will always be the same as the dipole in the radial direction and will be opposite to the direction in the perpendicular axis. The simplest example of an electric dipole is a pair of electric charges of two opposite signs and equal magnitude separated by distance.
Complete step by step solution:
It is given in the question that suppose $\vec P$ is an electric dipole with direction as shown in the figure now consider an axis inclined at an angle $\theta $ (refer figure) (the image has been rotated for understanding purpose)

The direction on the net electric field is given perpendicular to the dipole.
So, for this, we need to find out, so we need to find the angle $\theta $ on the dipole up to which the axis is inclined.
So for this, we bifurcate the dipole $\vec P$ and take its component along the inclined axis and the axis perpendicular to it (refer figure)

So the component along the inclined axis will be $\vec P\cos \theta $ and the other component will be $\vec P\sin \theta $.
Now for our ease, we will treat the component $\vec P\cos \theta $ as a single dipole.
Now,
As we know if $\vec X$ be a dipole along the x-axis so electric field along that axis at a distance $r$ due to the dipole is given as:
${\vec E_r} = \dfrac{{2k\vec X}}{{{r^3}}}$
and its direction will be the same as the dipole direction.
Due to this as we know there will also be an electrical field in the equatorial plane and perpendicular to it will be given by
${\vec E_p} = \dfrac{{k\vec X}}{{{r^3}}}$
and its direction will be opposite to that of the initial field
See figure

Similarly, the electrical field along the direction of $\vec P\cos \theta $ will be

Here the value of $\vec P$ will be $\vec P\cos \theta $
so electrical field will be ${\vec E_r} = \dfrac{{2k\vec P\cos \theta }}{{{r^3}}}$
And now along its equatorial plane at the perpendicular axis, the value of electrical field will be ${\vec E_p} = \dfrac{{k\vec P\sin \theta }}{{{r^3}}}$
Now here the value of $\vec P$ will be $\vec P\sin \theta $ because the field in that direction is caused by the component $\vec P\sin \theta $ of dipole $\vec P$ so it will be in the equatorial plane of the dipole perpendicular to the initial field and opposite direction.
So now the resultant of these two fields will be somewhere between them let it be at an angle $\alpha $.
Now,
Using trigonometry
$
\operatorname{tan} \alpha = \dfrac{{\overrightarrow {{E_p}} }}{{\overrightarrow {{E_r}} }} \\
\therefore \operatorname{tan} \alpha = \dfrac{{\left( {\dfrac{{k\vec P\sin \theta }}{{{r^3}}}} \right)}}{{\left( {\dfrac{{2k\vec P\cos \theta }}{{{r^3}}}} \right)}} \\
\Rightarrow \operatorname{tan} \alpha = \dfrac{{\sin \theta }}{{2\cos \theta }} \\
\Rightarrow \operatorname{tan} \alpha = \dfrac{{\tan \theta }}{2} \\
$
$ \Rightarrow \operatorname{tan} \theta = 2\operatorname{tan} \alpha $___________________(1)
Now as we need to find $\theta $ so we need to eliminate $\alpha $and make in term of $\theta $
So as we can see in the question it is given that the net of the electric field should be perpendicular to the dipole so we extend the resultant line.

Refer triangle $\vartriangle ABC$ here we can hat the angle $\theta $ will be equal $\angle ABC$ due to the vertically opposite angle
$\vartriangle ABC$ is a right angle triangle so we can say that
$
\theta + \alpha = 90^\circ \\
\theta = 90^\circ - \alpha \\
$
So taking $\operatorname{tan} $ on both sides we get
$\operatorname{tan} \theta = \operatorname{tan} \left( {90 - \alpha } \right)$
Or $\operatorname{tan} \theta = cot\alpha $__________________(2)
The value $cot\alpha $ can be calculated from equation (1)
$
\because \operatorname{tan} \theta = 2\operatorname{tan} \alpha \\
\therefore cot\alpha = \dfrac{2}{{\operatorname{tan} \theta }} \\
$
So, substituting it in the above equation (2)
$
\operatorname{tan} \theta = \dfrac{2}{{\operatorname{tan} \theta }} \\
\Rightarrow {\operatorname{tan} ^2}\theta = 2 \\
\Rightarrow \operatorname{tan} \theta = \sqrt 2 \\
\Rightarrow \theta = {\operatorname{tan} ^{ - 1}}\sqrt 2 \\
$
Final answer is (D), The value of $\theta $ will be ${\operatorname{tan} ^{ - 1}}\sqrt 2 $.
Note: The electric fields accompanying the electric dipole will always be perpendicular to each other. The direction of the electric field will always be the same as the dipole in the radial direction and will be opposite to the direction in the perpendicular axis. The simplest example of an electric dipole is a pair of electric charges of two opposite signs and equal magnitude separated by distance.
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

A point charge + 20mu C is at a distance 6cm directly class 12 physics JEE_Main

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




