Question

The electric field due to an electric dipole at a distance r from its center in axial position is E. If the dipole is rotated through an angle of ${{90}^{\circ }}$ about its perpendicular axis, the electric field at the same point will be
(a). $E$
(b). $\dfrac{E}{4}$
(c). $\dfrac{E}{2}$
(d). $2E$

Answer 1

- Hint: First let us learn about electric dipole and the net field created due to the dipole. An electric dipole deals with the separation of the positive and negative charges in an electromagnetic system. A pair of electric charges of equal magnitude but opposite signs separated by some small distance is an example for electric dipole.

Complete step-by-step solution -
We know that an electric charge produces an electric field around it. This electric field magnitude decreases with increase in distance from the charge producing that field. Hence, we can say that more the distance from the charged particle, less the magnitude of the electric field. The electric field at a point due to a charge is given by:
$E=\dfrac{kq}{{{r}^{2}}}$ , where E is the electrical field at the point, q is the charge, and r is the distance between the points.

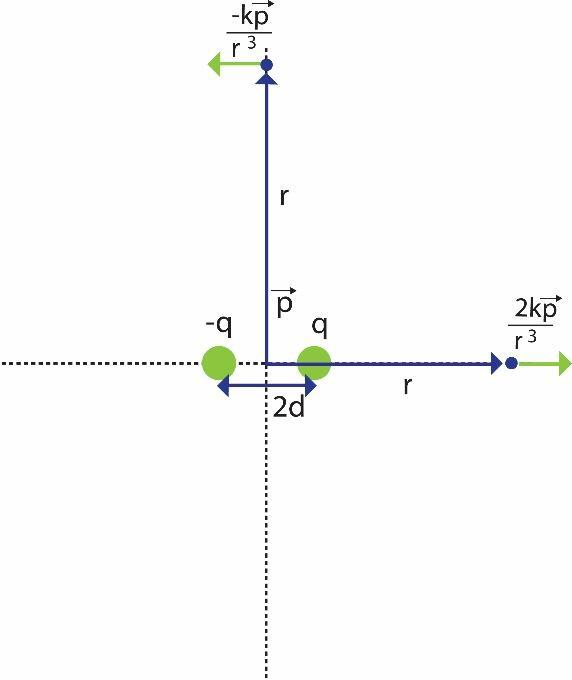
Two charges with equal magnitude and opposite charge separated by a distance is known as Electric dipole. The distance between the two oppositely charged particles is extremely small (assumed to be 2d) that both the electric fields produced will combine to produce net electric field. The center of the electric dipole is defined as the midpoint of the imaginary line between the two opposite charges. The axis of the dipole is the line joining both the charges. Refer to the figure.
The electric field due to an electric dipole at a distance r from its center in axial position is,
\[\begin{align}
  & E=\dfrac{kq}{{{(r-d)}^{2}}}-\dfrac{kq}{{{(r+d)}^{2}}}=\dfrac{kq[{{(r+d)}^{2}}-{{(r-d)}^{2}}]}{{{(r+d)}^{2}}{{(r-d)}^{2}}} \\
 & \Rightarrow \dfrac{kq[(r-d+r+d)(r+d-r+d)]}{{{(r+d)}^{2}}{{(r-d)}^{2}}}=\dfrac{kq(2r)(2d)}{{{(r+d)}^{2}}{{(r-d)}^{2}}} \\
 & \text{Since, }d << r: \\
 & E=\dfrac{kq(2r)(2d)}{{{r}^{4}}}=\dfrac{2kp}{{{r}^{3}}} \\
\end{align}\] … (1)

Where, \[k=9\times {{10}^{9}}\dfrac{N{{m}^{2}}}{{{C}^{2}}}\] is a constant. p is the value of dipole moment which is equal to the product of distance between the charges and magnitude of one of the charges.
$p=2qd$
The perpendicular axis of the dipole is the line perpendicular to the axial plane and passing through the midpoint of the dipole. Now, when the dipole is rotated by then the electric field (say $E'$ ) is given by:
\[\begin{align}
  & E'=-\dfrac{2kq\sin \theta }{({{r}^{2}}+{{d}^{2}})}=-\dfrac{2kq}{({{r}^{2}}+{{d}^{2}})}\dfrac{d}{{{({{r}^{2}}+{{d}^{2}})}^{\dfrac{1}{2}}}} \\
 & \text{Since, }d << r \\
 & \Rightarrow E'=-\dfrac{kq(2d)}{{{r}^{3}}}=-\dfrac{kp}{{{r}^{3}}} \\
\end{align}\]… (2)
Compare equation (1) and (2) to find out that $E'=\dfrac{E}{2}$
Therefore, the correct answer is option (c).

Note: You have to be clear that the distance between the opposite charges is very less when compared to r in the question. Don't confuse that electric field and dipole moment are scalars as only magnitude is mentioned in the answer. Both electric field and dipole moments are vector quantities.