Question

The electric potential due to an infinite sheet of positive charge density σ at a point located at a perpendicular distance Z from the sheet is (Assume ${V_0}$​ to be the potential at the surface of sheet) :
A. ${V_0}$
B. ${V_0} - \dfrac{{\sigma Z}}{{{\varepsilon _0}}}$
C. ${V_0} + \dfrac{{\sigma Z}}{{2{\varepsilon _0}}}$
D. ${V_0} - \dfrac{{\sigma Z}}{{2{\varepsilon _0}}}$

Answer 1

Hint: When we do any work against the conservative force then the work done by us will be stored in the form of potential energy in the system and potential energy increases. Along the direction of conservative force then potential energy of the system decreases.

Formula used:
${F_c} = - \dfrac{{dU}}{{dx}}$

Complete solution Step-by-Step:
Let us assume there is an object. We are displacing that object up very slowly which means at every instant we can assume its velocity will be zero. When we are moving an object upwards which means that we are displacing the object against the gravitational force. That literally means we are doing some work and according to conservation of energy that work will not go in vain. It will get converted in some form and that is nothing but in the form of potential energy.
If we clearly observe the above case, as the object is moving against gravity i.e as the work done by gravity is negative, the potential energy of the system is increasing.
Hence from the above relation we have the formula ${F_c} = - \dfrac{{dU}}{{dx}}$
${F_c}$ is conservative force and ‘U’ is the potential energy and negative sign indicates that along the direction of conservative force, potential energy of the system decreases.
Similarly electrostatic force is also conservative force.
$\eqalign{
  & {F_c} = Eq \cr
  & \Rightarrow U = qV \cr
  & \Rightarrow {F_c} = - \dfrac{{dU}}{{dx}} \cr
  & \Rightarrow Eq = - \dfrac{{d\left( {qV} \right)}}{{dx}} \cr
  & \therefore E = - \dfrac{{dV}}{{dx}} \cr} $
Electric field due to the sheet is given as $\dfrac{{\sigma Z}}{{2{\varepsilon _0}}}$.

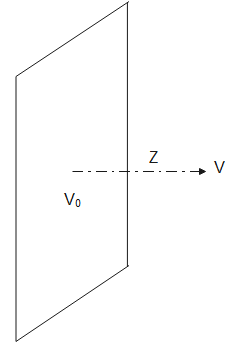
The above diagram depicts the sheet of positive charge and ${V_0}$ is the potential of the surface and V is the potential at distance ‘Z’ from the surface and it is given that sigma is surface charge density.
From the above potential formula, we have
$\eqalign{
  & E = - \dfrac{{dV}}{{dx}} \cr
  & \Rightarrow \int\limits_{{V_0}}^V {dV} = - E\int\limits_0^Z {dZ} \cr
  & \Rightarrow V - {V_0} = - \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {Z - 0} \right] \cr
  & \therefore V = {V_0} - \dfrac{{\sigma Z}}{{2{\varepsilon _0}}} \cr} $

Hence, option D is correct.

Note:
Potential energy is valid only if conservative forces are present. Gravity, spring force and electrostatic force are the examples for conservative forces. In the question it doesn’t matter which coordinates they give, the electric field depends only upon the perpendicular distance from the sheet.