Question

The end points of a body diagonal of a rectangular parallelepiped whose faces are parallel to the coordinate planes are (2,3,5) and (5,7,10). The length of its sides are
\[\begin{align}
  & A.5,7,3 \\
 & B.6,5,3 \\
 & C.3,6,2 \\
 & D.3,4,5 \\
\end{align}\]

Answer 1

Hint: In this question, we need to find the length of side of a parallelepiped whose faces are parallel to the coordinate plane and end points of body diagonal are (2,3,5) and (5,7,10). For this, we will first draw parallelepiped having length l, breadth b and height h and label the known coordinate. Then using (2,3,5) and (5,7,10) we will form an equation of parallel faces of the parallelepiped and then calculate distance between them. These distances will be the length of the sides.

Complete step-by-step answer:
Here, end points of body diagonal of rectangular parallelepiped are (2,3,5) and (5,7,10). Since faces are parallel to coordinate planes, so our parallelepiped will look like this,

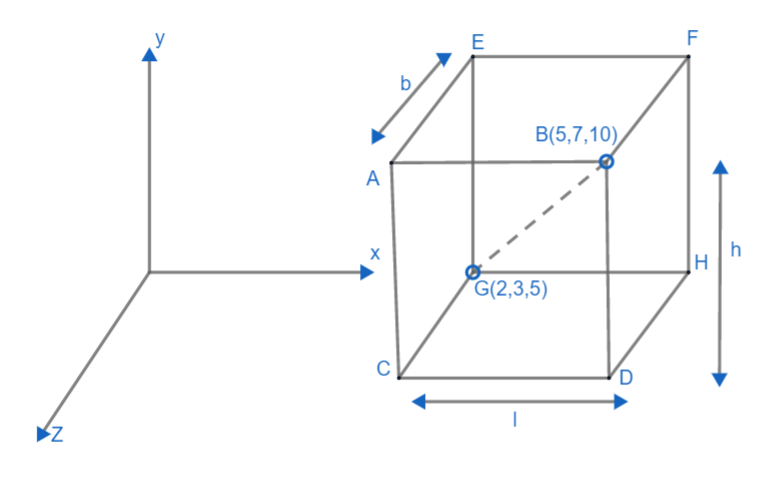
As we can see from diagram, faces AECG and BDHF are corresponding to planes of x coordinate in the yz plane. Therefore, AECG will be equal to the plane x = 2 (from (2,3,5)) and BFDH will be equal to the plane x = 5 (from (5,7,10)). Also, faces CDHG and AEFB are corresponding to the plane of x coordinate in the xz plane. Therefore, CDHG will be equal to the plane y = 3 (from (2,3,5)) and AEFG will be equal to the plane y = 7 (from (5,7,10)). Similarly, faces ABDC and EFHG are corresponding to planes of z coordinate in the xy plane. Therefore, ABDC will be equal to the plane z = 5 (from (2,3,5)) and EFHG will be equal to the plane z = 10 (from (5,7,10)). We need to find the length of the side, so distant between planes AECG and BFDH will give us length of GH or CD or EF or AB. Hence, l will be equal to 5-2 = 3.
Hence the length of parallelepiped is 3.
Distance between planes CDHG and AEFB will give us length of AC, BD, EG, FH. Hence h will be equal to 7-3 = 4.
Hence the height of the parallelepiped is 4.
Distance between planes ABDC and EFHG will give us length of AE, BF, CG, HD. Hence, b will be equal to 10-5 = 5.
Hence breadth of the parallelepiped is 5.
So, sides of parallelepiped are 3, 4, 5.

So, the correct answer is “Option D”.

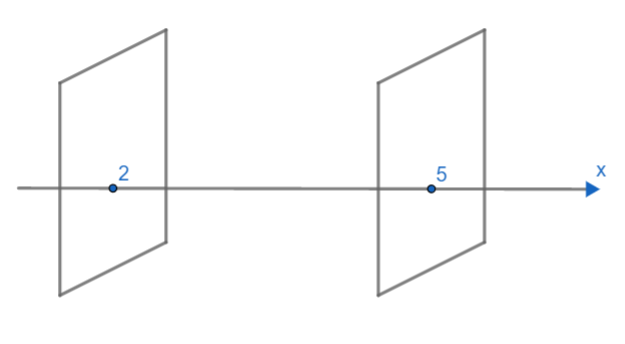
Note: Students should note that we have taken the equation of plane x = 2 or x = 5 and so on because it is given that all these faces are parallel to the coordinate plane. Students can get confused between planes and distance. They can also draw individual diagrams to understand clearly. For example: for x = 2 or x = 5 faces are,