Question

The ends Q and R of two thin wires, PQ and RS, are soldered (joined) together. Initially each of the wires has a length of 1 m at 10°C. Now the end P is maintained at 10°C, while the end S is heated and maintained at 400°C. The system is thermally insulated from its surroundings. If the thermal conductivity of wire PQ is twice RS and the coefficient of linear thermal expansion of PQ is $1.2\quad \times \quad { 10 }^{ -5 }\quad { K }^{ -1 }$, the change in length of the wire PQ is:
A.)0.78mm
B.)0.90mm
C.)1.56mm
D.)2.34mm

Answer 1

Hint: Rate of heat flow from the end S to R is equal to the rate of heat flow from the end Q to P. Using this relation find the temperature at junction of Q and R. Using this temperature calculate temperature gradient across wire PQ. Then, find the change in length of the wire using the relation between increase in length of small length, coefficient of linear thermal expansion and temperature gradient.

Formula used:
$\dfrac { { Q } }{ t } =\dfrac { kA({ T }_{ 2 }-{ T }_{ 1 }) }{ x }$
$\dfrac { \Delta T }{ \Delta x } =\quad \dfrac { T\quad -\quad { T }_{ 1 } }{ \Delta x }$
$\dfrac { dl }{ dx } =\quad \alpha \Delta T$

Complete answer:
Given: x = 1m
             ${ T }_{ 1 }=\quad 10℃$
             ${ T }_{ 2 }=\quad 100℃$

Let the temperature at the junction of Q and R be T.

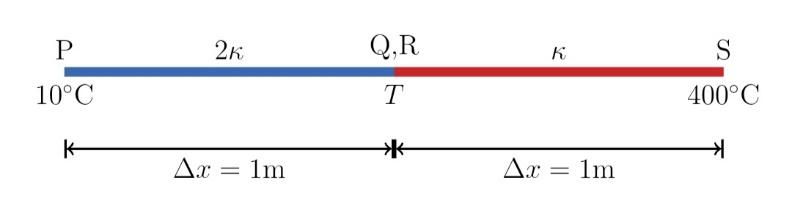
As the system is insulated from the surrounding, the rate of flow of heat from the end S to R is equal to the rate of flow of heat from the end Q to P.
$\therefore \dfrac { d{ Q }_{ SR } }{ dt } =\dfrac { d{ Q }_{ QP } }{ dt }$ …(1)
Formula for rate of heat flow is given by,
$\dfrac { { Q } }{ t } =\dfrac { kA({ T }_{ 2 }-{ T }_{ 1 }) }{ x }$ …(2)

Now, differentiating equation.(2) and then substituting in equation.(1)
$\therefore \dfrac { kA({ T }_{ 2 }-{ T }_{ 1 }) }{ \Delta x } =\quad \dfrac { 2kA({ T }_{ 2 }-{ T }_{ 1 }) }{ \Delta x }$ …(3)

Substituting the values in equation.(3) we get,
$ \quad kA(400-T)\quad =\quad 2kA(T-10)$
$\therefore \quad 400-T\quad =\quad 2T-20$
$\therefore T\quad =\quad 140℃$

Now, the temperature gradient across wire PQ is given by,
$\dfrac { \Delta T }{ \Delta x } =\quad \dfrac { T\quad -\quad { T }_{ 1 } }{ \Delta x }$
By substituting the values we get,
$\dfrac { \Delta T }{ \Delta x } =\quad \dfrac { 140\quad -\quad 10 }{ 1 }$
$\therefore \quad \Delta T=\quad 130\Delta x$

Increase in length of small element $\Delta x$ is given by,
$\dfrac { dl }{ dx } =\quad \alpha \Delta T$
$\therefore \quad dl=\quad \alpha \Delta Tdx$ …(4)
where, $\alpha$: coefficient of linear expansion

$\therefore \quad dl=\quad \alpha dx(130x)$
Now, by integrating both the sides we get,
$\therefore \quad \Delta l=\quad \dfrac { 130\alpha { x }^{ 2 } }{ 2 }$
Then by substituting the values we get,
$\Delta l=\quad \dfrac { 130\times 1.2\times { 10 }^{ -5 }\times 1 }{ 2 }$
$\therefore \quad \Delta l=\quad 78\quad \times \quad { 10 }^{ -5 }\quad m$
$\therefore \quad \Delta l=\quad 0.78mm$
Therefore, the change in length of the wire PQ is 0.78mm.

So, the correct answer is “Option A”.

Note:
As the system is insulated from the surrounding, the rate of flow of heat from the end S to R is equal to the rate of flow of heat from the end Q to P. But if the system was either open or closed, the rate of flow of heat would not be the same.