Question

The equation of ellipse with center at origin and major axis along x-axis is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Find the length of the major axis.

Answer 1

Hint: we know that for an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ the end points of vertex is (a, 0) and (-a, 0). Hence we can easily find the distance between two points. This distance is nothing but the length of the major axis.

Complete step by step answer:
Now we know that the equation $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ represents an ellipse with major axis along x axis.

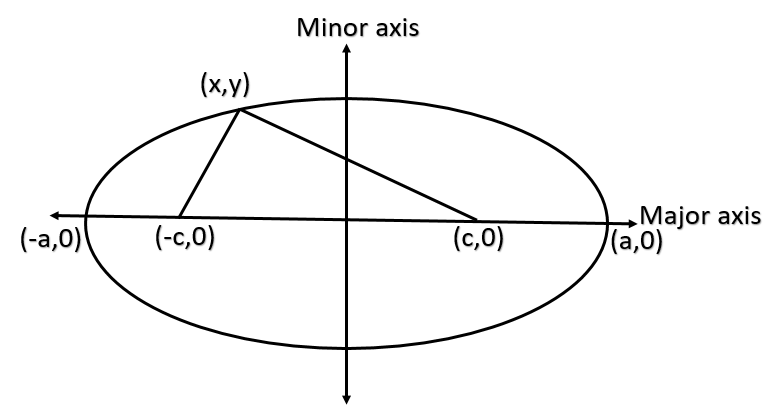
Now in an ellipse the longer axis is called major axis and the shorter axis is called minor axis.
The endpoints of major axis are called the vertex of ellipse and similarly the end points of minor axis are called co-vertex of ellipse.
The point where axis intersect is called center of ellipse.
Now the foci of ellipse always lies on the major axis of ellipse.
By definition of ellipse sum of distance any point on ellipse with both its foci is constant.
Now for equation of ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ the vertex are given by (a, 0) and (-a, 0).
Now we can easily prove this by substituting y = 0 in the equation of ellipse.
Now we know that distance between two points (a, 0) and (b, 0) on x-axis is given by |a – b|
Hence the distance between two vertex is |a – (–a)| = |a + a| = 2a

Hence the distance between two vertices is 2a.

Note: Note that the points (0, b) and (0, - b) are the co-vertex of the ellipse and not the vertex of the ellipse vertex is always calculated with respect to the major axis.