
The equation of progressive wave is $y=0.2\sin 2\pi \left[ \dfrac{t}{0.01}-\dfrac{x}{0.3} \right]$, where $x$ and $y$ are in metre and $t$ is in seconds. The velocity of the wave is
$\text{A}\text{. }30m{{s}^{-1}}$
$\text{B}\text{. }40m{{s}^{-1}}$
$\text{C}\text{. }300m{{s}^{-1}}$
$\text{D}\text{. }400m{{s}^{-1}}$
Answer
486k+ views
Hint: For calculating velocity of a progressive wave we need to compare the given equation with the standard equation of progressive wave. Then we can find values of coefficient of time $t$ and coefficient of distance covered $x$ and dividing them will give the value of velocity of wave.
Formulae used:
$y=a\sin 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right)$
$\text{Velocity of wave = }\dfrac{\text{coefficient of t}}{\text{coefficient of x}}$
Complete step by step answer:
A progressive wave is a type of wave which travels from a specific point A in the medium to another point B. We can say that a wave that is continuously in motion in the same direction without change in its amplitude is known as a progressive wave, or a travelling wave.
A progressive wave has two points at a given phase, crest or dip which travel forwards while the other point is medium which remains in the same position where it is.
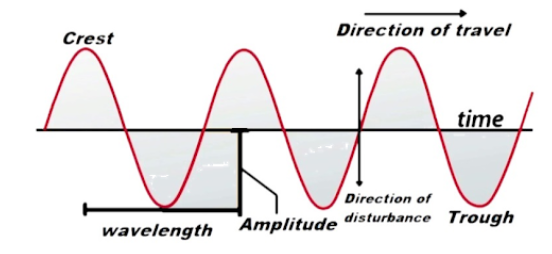
Equation of a plane progressive wave is given by:
$y=a\sin 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right)$
Where,
$y$ is the displacement of particle at given instant of time
$a$ is the amplitude of vibration of the particle
$\lambda $ is taken as the distance between two particles or the wavelength of wave
$x$ is the distance of particle from origin
$t$ is instantaneous time
$T$ is the time period of oscillation of vibration of particle
For the propagation of waves, one point moves to the place of another point. If we observe, the phase of point $X$ remains the same throughout the propagation. Also, the velocity of the wave transmission is actually the velocity with which point $X$ is moving.
$2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right)=\phi $
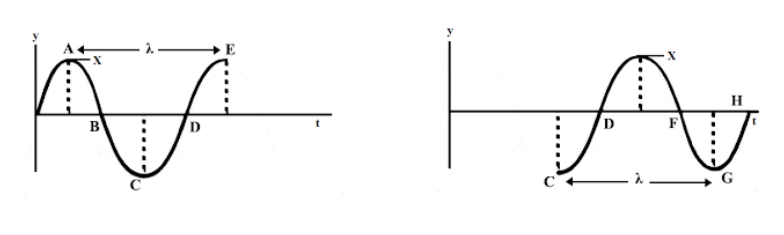
For a particular point $X$, $\phi $ remains constant
Therefore,
$\dfrac{d\left[ 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right) \right]}{dt}=\dfrac{d\phi }{dt}=0$
$\Rightarrow 2\pi \left[ \dfrac{1}{T}-\dfrac{dx}{dt}\cdot \dfrac{1}{\lambda } \right]=0$
We get,
$\dfrac{dx}{dt}=\dfrac{\lambda }{T}$
Or,
\[\dfrac{dx}{dt}=\dfrac{\left( \dfrac{1}{T} \right)}{\left( \dfrac{1}{\lambda } \right)}=\dfrac{\text{coefficient of }t}{\text{coefficient of }x}\]
Considering the standard equation of progressive wave,
Wavelength of the wave $\lambda $ comes in the denominator of $x$, while the time period of oscillation $T$ comes in the denominator of $t$.
For finding velocity of wave, we need to find the coefficient of $x$ and coefficient of $t$.
$\text{Velocity of wave = }\dfrac{\text{coefficient of t}}{\text{coefficient of x}}$
$v=\dfrac{\dfrac{2\pi }{0.01}}{\dfrac{2\pi }{0.3}}=30\dfrac{m}{s}$
Velocity of given progressive wave is $30m{{s}^{-1}}$
Hence, the correct option is A.
Note: Students should not get confused between particle velocity and wave velocity. In the above question, we calculated the velocity of the wave. For calculating particle velocity we can use the formula, ${{v}_{P}}=-v\dfrac{dy}{dx}$, where, ${{v}_{P}}$ is the particle velocity and $v$ is the wave velocity. Also, it should be kept in mind that the velocity of the wave is the division of wavelength and time period, thus, velocity of a progressive wave can be expressed as the coefficient of $t$ divided by coefficient of $x$.
Formulae used:
$y=a\sin 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right)$
$\text{Velocity of wave = }\dfrac{\text{coefficient of t}}{\text{coefficient of x}}$
Complete step by step answer:
A progressive wave is a type of wave which travels from a specific point A in the medium to another point B. We can say that a wave that is continuously in motion in the same direction without change in its amplitude is known as a progressive wave, or a travelling wave.
A progressive wave has two points at a given phase, crest or dip which travel forwards while the other point is medium which remains in the same position where it is.

Equation of a plane progressive wave is given by:
$y=a\sin 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right)$
Where,
$y$ is the displacement of particle at given instant of time
$a$ is the amplitude of vibration of the particle
$\lambda $ is taken as the distance between two particles or the wavelength of wave
$x$ is the distance of particle from origin
$t$ is instantaneous time
$T$ is the time period of oscillation of vibration of particle
For the propagation of waves, one point moves to the place of another point. If we observe, the phase of point $X$ remains the same throughout the propagation. Also, the velocity of the wave transmission is actually the velocity with which point $X$ is moving.
$2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right)=\phi $
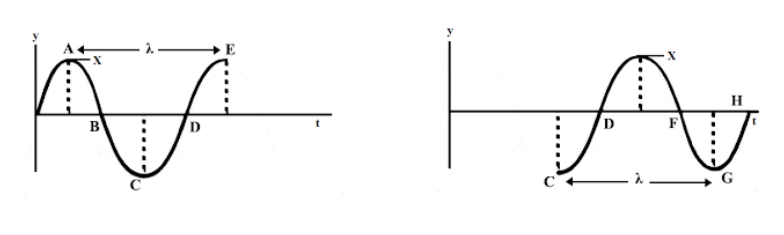
For a particular point $X$, $\phi $ remains constant
Therefore,
$\dfrac{d\left[ 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right) \right]}{dt}=\dfrac{d\phi }{dt}=0$
$\Rightarrow 2\pi \left[ \dfrac{1}{T}-\dfrac{dx}{dt}\cdot \dfrac{1}{\lambda } \right]=0$
We get,
$\dfrac{dx}{dt}=\dfrac{\lambda }{T}$
Or,
\[\dfrac{dx}{dt}=\dfrac{\left( \dfrac{1}{T} \right)}{\left( \dfrac{1}{\lambda } \right)}=\dfrac{\text{coefficient of }t}{\text{coefficient of }x}\]
Considering the standard equation of progressive wave,
Wavelength of the wave $\lambda $ comes in the denominator of $x$, while the time period of oscillation $T$ comes in the denominator of $t$.
For finding velocity of wave, we need to find the coefficient of $x$ and coefficient of $t$.
$\text{Velocity of wave = }\dfrac{\text{coefficient of t}}{\text{coefficient of x}}$
$v=\dfrac{\dfrac{2\pi }{0.01}}{\dfrac{2\pi }{0.3}}=30\dfrac{m}{s}$
Velocity of given progressive wave is $30m{{s}^{-1}}$
Hence, the correct option is A.
Note: Students should not get confused between particle velocity and wave velocity. In the above question, we calculated the velocity of the wave. For calculating particle velocity we can use the formula, ${{v}_{P}}=-v\dfrac{dy}{dx}$, where, ${{v}_{P}}$ is the particle velocity and $v$ is the wave velocity. Also, it should be kept in mind that the velocity of the wave is the division of wavelength and time period, thus, velocity of a progressive wave can be expressed as the coefficient of $t$ divided by coefficient of $x$.
Recently Updated Pages
Glucose when reduced with HI and red Phosphorus gives class 11 chemistry CBSE

The highest possible oxidation states of Uranium and class 11 chemistry CBSE

Find the value of x if the mode of the following data class 11 maths CBSE

Which of the following can be used in the Friedel Crafts class 11 chemistry CBSE

A sphere of mass 40 kg is attracted by a second sphere class 11 physics CBSE

Statement I Reactivity of aluminium decreases when class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

The correct order of melting point of 14th group elements class 11 chemistry CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

What organs are located on the left side of your body class 11 biology CBSE




