Question

The equation of the circumcircle of an equilateral triangle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ and one vertex of the triangle is (1, 1). The equation of the incircle of the triangle is
(a) $4\left( {{x}^{2}}+{{y}^{2}} \right)={{g}^{2}}+{{f}^{2}}$
(b) $4\left( {{x}^{2}}+{{y}^{2}} \right)+8gx+8fy=\left( 1-g \right)\left( 1+3g \right)+\left( 1-f \right)\left( 1+3f \right)$
(c) $4\left( {{x}^{2}}+{{y}^{2}} \right)+8gx+8fy={{g}^{2}}+{{f}^{2}}$
(d) None of these

Answer 1

Hint: To solve this question, we will first draw the figure of the circumcircle, the equilateral triangle and the incircle. Then we will define standard properties of a circle and circumcircle and incircle of an equilateral triangle use those results to find the equation of the incircle. It is given that (1, 1) is a vertex of the triangle. This means it lies on the circumcircle. We will substitute (1, 1) in the equation to find one of the variables in the form of another.

Complete step-by-step answer:
It is given that the equation of the circumcircle of an equilateral triangle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. It is given that point (1, 1) is a vertex of the triangle and so it lies on this circle.
We are supposed to find the equation of the incircle of the triangle.
Now, from the concepts of circle and coordinate geometry, we know that the centre of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is $\left( -g,-f \right)$.
We also know that the radius of circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Now, in the case of equilateral triangle, we know that the centre of circumcircle and centre of circumcircle coincide.
So, if the centre of the circumcircle of an equilateral triangle is $\left( -g,-f \right)$, then the centre of that equilateral triangle is also $\left( -g,-f \right)$.
The figure of circumcircle, equilateral triangle and incircle will as follows:

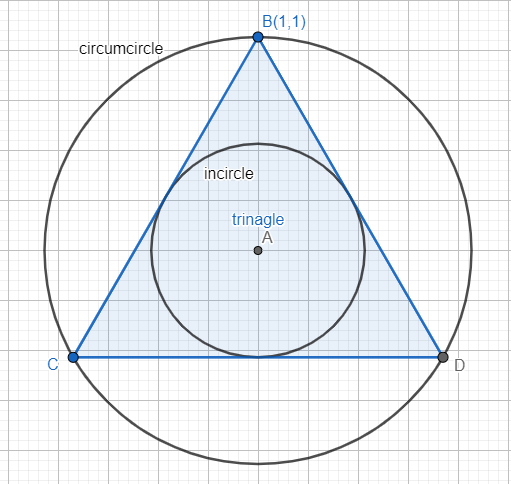
As we can see in the figure, BCD is the equilateral triangle with an incline and circumcentre as A and B(1, 1) lies on the circumcircle.
We will substitute (1, 1) in the equation of the circumcircle to find the value of c.
$\begin{align}
  & \Rightarrow {{\left( 1 \right)}^{2}}+{{\left( 1 \right)}^{2}}+2g\left( 1 \right)+2f\left( 1 \right)+c=0 \\
 & \Rightarrow c=-\left( 2+2g+2f \right) \\
\end{align}$
From the properties of circumcircle and incircle of a triangle, we also know that the radius of the incircle is half that of circumcircle.
Let r be the radius of the incircle.
$\begin{align}
  & \Rightarrow r=\dfrac{1}{2}\sqrt{{{g}^{2}}+{{f}^{2}}-c} \\
 & \Rightarrow r=\dfrac{1}{2}\sqrt{{{g}^{2}}+{{f}^{2}}-\left[ -\left( 2+2g+2f \right) \right]} \\
 & \Rightarrow r=\dfrac{1}{2}\sqrt{{{g}^{2}}+{{f}^{2}}+2g+2f+2} \\
\end{align}$
Now, equation of any circle with centre (a, b) is given as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$, where r is the radius of the circle.
Therefore, equation of the circle with centre $\left( -g,-f \right)$ and radius $r=\dfrac{1}{2}\sqrt{{{g}^{2}}+{{f}^{2}}+2g+2f+2}$ will be as follows:
$\Rightarrow {{\left( x+g \right)}^{2}}+{{\left( y+f \right)}^{2}}=\dfrac{1}{4}\left( {{g}^{2}}+{{f}^{2}}+2g+2f+2 \right)$
We will now simplify the equation and see which of the options matches the simplified equation.
$\begin{align}
  & \Rightarrow {{x}^{2}}+{{g}^{2}}+2gx+{{y}^{2}}+{{f}^{2}}+2fy=\dfrac{1}{4}\left( {{g}^{2}}+{{f}^{2}}+2g+2f+2 \right) \\
 & \Rightarrow 4\left( {{x}^{2}}+{{y}^{2}} \right)+4{{g}^{2}}+8gx+4{{f}^{2}}+8fy=\left( {{g}^{2}}+{{f}^{2}}+2g+2f+2 \right) \\
 & \Rightarrow 4\left( {{x}^{2}}+{{y}^{2}} \right)+8gx+8fy=1-3{{g}^{2}}+2g+1-3{{f}^{2}}+2f \\
 & \Rightarrow 4\left( {{x}^{2}}+{{y}^{2}} \right)+8gx+8fy=\left( 1-g \right)\left( 1+3g \right)+\left( 1-f \right)\left( 1+3f \right) \\
\end{align}$

So, the correct answer is “Option b”.

Note: Students are advised to be aware of the options. We can see no option had the term c, that is the reason why we substituted c and not any other variable. The question requires understanding of the intermediate level geometry of triangles and circles.