Question

The equation of the line of shortest distance between the lines \[\dfrac{x+4}{4}=\dfrac{y-2}{-2}=\dfrac{z-3}{0}\] and \[\dfrac{x-5}{5}=\dfrac{y-3}{3}=\dfrac{z}{0}\], is
\[\begin{align}
  & (A)\text{ }\dfrac{x+4}{0}=\dfrac{y-2}{0}=\dfrac{z-3}{1} \\
 & (B)\text{ }\dfrac{x-5}{0}=\dfrac{y-3}{0}=\dfrac{z}{1} \\
 & (C)\text{ }\dfrac{x}{0}=\dfrac{y}{0}=\dfrac{z-3}{1} \\
 & (D)\text{ None of these} \\
\end{align}\]

Answer 1

Hint: We needed to remember that the line of shortest distance between lines \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] is \[{{L}_{3}}:\dfrac{x-{{x}_{3}}}{{{a}_{3}}}=\dfrac{y-{{y}_{3}}}{{{b}_{3}}}=\dfrac{z-{{z}_{3}}}{{{c}_{3}}}\] which must be perpendicular and also passes through the both \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\]. By this point, we can solve the problem. Now we should equate \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] to a constant \[\lambda \]. In the similar way, we should equate \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] to a constant \[\mu \]. Now we should find the line passing through these two points. Let us assume this line as \[{{L}_{3}}:\dfrac{x-{{x}_{3}}}{{{a}_{3}}}=\dfrac{y-{{y}_{3}}}{{{b}_{3}}}=\dfrac{z-{{z}_{3}}}{{{c}_{3}}}\]. This line should be perpendicular to both \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] This will give us the \[{{L}_{3}}:\dfrac{x-{{x}_{3}}}{{{a}_{3}}}=\dfrac{y-{{y}_{3}}}{{{b}_{3}}}=\dfrac{z-{{z}_{3}}}{{{c}_{3}}}\]. Now by using the concept of sum of product of directional ratios of perpendicular will be zero, we can find the values of both \[\lambda \] and \[\mu \].

Complete step-by-step solution:
From the given information, let us assume \[{{L}_{1}}:\dfrac{x+4}{4}=\dfrac{y-2}{-2}=\dfrac{z-3}{0}\] and \[{{L}_{2}}:\dfrac{x-5}{5}=\dfrac{y-3}{3}=\dfrac{z}{0}\].
Let \[{{L}_{1}}:\dfrac{x+4}{4}=\dfrac{y-2}{-2}=\dfrac{z-3}{0}=\lambda .....(1)\]
From the equation (1) we get
\[\dfrac{x+4}{4}=\lambda \]
By using cross multiplication, we get
\[\Rightarrow x=4\lambda -4......(2)\]
In the same way, from equation (1) we get
\[\dfrac{y-2}{-2}=\lambda \]
By using cross multiplication, we get
\[\Rightarrow y=-2\lambda +2......(3)\]
In the same way, from equation (3) we get
\[\dfrac{z-3}{0}=\lambda \]
By using cross multiplication, we get
\[\Rightarrow z=3......(4)\]
From equation (2), (3) and (4) let us assume a point on \[{{L}_{1}}:\dfrac{x+4}{4}=\dfrac{y-2}{-2}=\dfrac{z-3}{0}\]is \[A\left( 4\lambda -4,-2\lambda +2,3 \right)\].
Let \[{{L}_{2}}:\dfrac{x-5}{5}=\dfrac{y-3}{3}=\dfrac{z}{0}=\mu ....(5)\]
From the equation (5) we get
\[\dfrac{x-5}{5}=\mu \]
By using cross multiplication, we get
\[\Rightarrow x=5\mu +5.....(6)\]
In the same way, from equation (5) we get
\[\dfrac{y-3}{3}=\mu \]
By using cross multiplication, we get
\[\Rightarrow y=3\mu +3.....(7)\]
In the same way, from equation (5) we get
\[\dfrac{z}{0}=\mu \]
By using cross multiplication, we get
\[\Rightarrow z=0......(8)\]
From equation (5), (6) and (7) let us assume a point on \[{{L}_{2}}:\dfrac{x-5}{5}=\dfrac{y-3}{3}=\dfrac{z}{0}=\mu ....(5)\] is \[B\left( 5\mu +5,3\mu +3,0 \right)\].
We know that the equation of line passing through \[A\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\] and \[B\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\] is \[\dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\dfrac{z-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}} \]
Now we can find the equation of line passing through \[A\left( 4\lambda -4,-2\lambda +2,3 \right)\] and \[B\left( 5\mu +5,3\mu +3,0 \right)\] is \[{{L}_{3}}:\dfrac{x-(4\lambda -4)}{\left( 5\mu +5 \right)-\left( 4\lambda -4 \right)}=\dfrac{y-\left( -2\lambda +2 \right)}{\left( 3\mu +3 \right)-\left( -2\lambda +2 \right)}=\dfrac{z-3}{0-3}\]
\[\Rightarrow {{L}_{3}}:\dfrac{x-4\lambda +4}{\left( 5\mu -4\lambda +9 \right)}=\dfrac{y+2\lambda -2}{\left( 2\lambda +3\mu +1 \right)}=\dfrac{z-3}{-3}\]
We know that the line of shortest distance between lines \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] is \[{{L}_{3}}:\dfrac{x-{{x}_{3}}}{{{a}_{3}}}=\dfrac{y-{{y}_{3}}}{{{b}_{3}}}=\dfrac{z-{{z}_{3}}}{{{c}_{3}}}\]which must be perpendicular to both }\[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\].

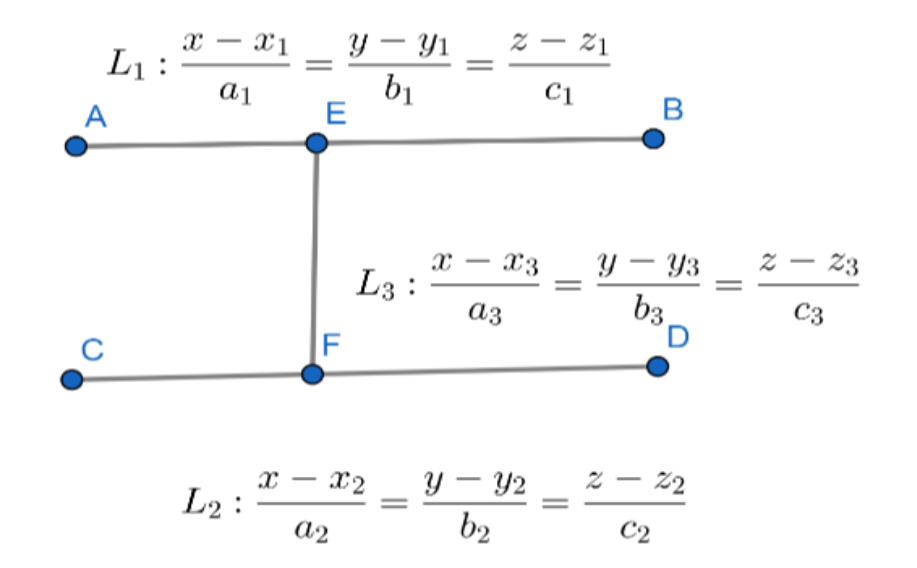
From the above condition, we get
\[{{L}_{3}}:\dfrac{x-4\lambda +4}{\left( 5\mu -4\lambda +9 \right)}=\dfrac{y+2\lambda -2}{\left( 2\lambda +3\mu +1 \right)}=\dfrac{z-3}{-3}\]is perpendicular to both \[{{L}_{1}}:\dfrac{x+4}{4}=\dfrac{y-2}{-2}=\dfrac{z-3}{0}\] and \[{{L}_{2}}:\dfrac{x-5}{5}=\dfrac{y-3}{3}=\dfrac{z}{0}\]
We know that a line \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] is said to be perpendicular to \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] , if \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\].
So, Line\[{{L}_{3}}:\dfrac{x-4\lambda +4}{\left( 5\mu -4\lambda +9 \right)}=\dfrac{y+2\lambda -2}{\left( 2\lambda +3\mu +1 \right)}=\dfrac{z-3}{-3}\] should be perpendicular to \[{{L}_{1}}:\dfrac{x+4}{4}=\dfrac{y-2}{-2}=\dfrac{z-3}{0}\].
We get \[{{a}_{1}}=5\mu -4\lambda +9,{{b}_{1}}=\left( 2\lambda +3\mu +1 \right),{{c}_{1}}=-3\] and \[{{a}_{2}}=4,{{b}_{2}}=-2,{{c}_{2}}=0\].
\[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\]
\[\Rightarrow 4\left( 5\mu -4\lambda +9 \right)+(-2)\left( 2\lambda +3\mu +1 \right)+3(0)=0\]
\[\Rightarrow 20\mu -16\lambda +36-4\lambda -6\mu -2=0\]
\[\Rightarrow -20\lambda +14\mu +34=0\]
\[\Rightarrow 20\lambda -14\mu -34=0\]
\[\Rightarrow 10\lambda -7\mu -17=0.....(9)\]
In the similar manner, we know that line\[{{L}_{3}}:\dfrac{x-4\lambda +4}{\left( 5\mu -4\lambda +9 \right)}=\dfrac{y+2\lambda -2}{\left( 2\lambda +3\mu +1 \right)}=\dfrac{z-3}{-3}\] should be perpendicular to \[{{L}_{2}}:\dfrac{x-5}{5}=\dfrac{y-3}{3}=\dfrac{z}{0}\].
We get \[{{a}_{1}}=5\mu -4\lambda +9,{{b}_{1}}=\left( 2\lambda +3\mu +1 \right),{{c}_{1}}=-3\] and \[{{a}_{2}}=5,{{b}_{2}}=3,{{c}_{2}}=0\].
\[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\]
\[\Rightarrow 5\left( 5\mu -4\lambda +9 \right)+(3)\left( 2\lambda +3\mu +1 \right)+3(0)=0\]
\[\Rightarrow 25\mu -20\lambda +45+6\lambda +9\mu +3=0\]
\[\Rightarrow -14\lambda +34\mu +48=0\]
\[\Rightarrow 14\lambda -34\mu -48=0\]
\[\Rightarrow 7\lambda -17\mu -24=0.....(10)\]
We need to find the values of \[\lambda \] and \[\mu \], to get the equation of line \[{{L}_{3}}:\dfrac{x-4\lambda +4}{\left( 5\mu -4\lambda +9 \right)}=\dfrac{y+2\lambda -2}{\left( 2\lambda +3\mu +1 \right)}=\dfrac{z-3}{-3}\].
By solving equations (9) and (10) we will get the values of \[\lambda \] and \[\mu \].
We should multiply equation (9) by 7.
\[70\lambda -49\mu -119=0....(11)\]
We should multiply (10) by 10.
\[70\lambda -170\mu -240=0.....(12)\]
Now we should subtract (11) and (12).
\[\begin{align}
  & \left( 70\lambda -49\mu -119 \right)-\left( 70\lambda -170\mu -240 \right)=0 \\
 & \Rightarrow (170-49)\mu +(240-119)=0 \\
 & \Rightarrow 121\mu +121=0 \\
 & \Rightarrow 121\mu =-121 \\
 & \Rightarrow \mu =-1....(13) \\
\end{align}\]
From equation (13) we get the value of \[\mu \],
Now we will substitute the value of \[\mu \]in (10).
\[\begin{align}
  & 7\lambda -17(-1)-24=0 \\
 & \Rightarrow 7\lambda +17-24=0 \\
 & \Rightarrow 7\lambda -7=0 \\
 & \Rightarrow \lambda =1.......(14) \\
\end{align}\]
From equation (14) we get the value of \[\lambda \].
Now we will substitute the both values of \[\lambda \] and \[\mu \]in line equation \[{{L}_{3}}:\dfrac{x-4\lambda +4}{\left( 5\mu -4\lambda +9 \right)}=\dfrac{y+2\lambda -2}{\left( 2\lambda +3\mu +1 \right)}=\dfrac{z-3}{-3}\].
\[\Rightarrow {{L}_{3}}:\dfrac{x-4(1)+4}{\left( 5(-1)-4(1)+9 \right)}=\dfrac{y+2(1)-2}{-\left( 2(1)+3(-1)+1 \right)}=\dfrac{z-3}{-3}\]
\[\Rightarrow {{L}_{3}}:\dfrac{x-4+4}{-5-4+9}=\dfrac{y+2-2}{(2-3+1)}=\dfrac{z-3}{-3}\]
\[\Rightarrow {{L}_{3}}:\dfrac{x-0}{0}=\dfrac{y-0}{0}=\dfrac{z-3}{-3}\]
Now we will multiply and divide the equation by (-3)
\[\Rightarrow {{L}_{3}}:\dfrac{x-0}{\left( \dfrac{0}{-3} \right)}=\dfrac{y-0}{\left( \dfrac{0}{-3} \right)}=\dfrac{z-3}{\left( \dfrac{-3}{-3} \right)}\]
\[\Rightarrow {{L}_{3}}:\dfrac{x-0}{0}=\dfrac{y-0}{0}=\dfrac{z-3}{1}\]
Hence, option (C) is correct.

Note: The formula to calculate the shortest distance between the lines between \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] is equal to \[\dfrac{\left| \left. \begin{align}
  & ({{x}_{2}}-{{x}_{1}}\text{) (}{{\text{y}}_{2}}-{{y}_{1}})\text{ (}{{\text{z}}_{2}}-{{z}_{1}}) \\
 & \text{ }{{\text{a}}_{1}}\;\;\;\;\;\;\;\;\;\;\;\;\; {{\text{b}}_{1}}\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;{{\text{c}}_{1}} \\
 & \text{ }{{\text{a}}_{2}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\text{b}}_{2}}\;\;\;\;\;\;\;\;\;\;\;\;\;\; {{\text{c}}_{2}} \\
\end{align} \right| \right.}{\sqrt{{{({{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}})}^{2}}+{{({{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}})}^{2}}+{{({{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}})}^{2}}}}\] where \[({{a}_{1}},{{b}_{1}},{{c}_{1}})\] and \[({{a}_{2}},{{b}_{2}},{{c}_{2}})\] are directional ratios of \[{{L}_{1}}:\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}}\] and \[{{L}_{2}}:\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] respectively.