
The expression of the number of visible maxima which are obtained through above said arrangement will turn out to be:
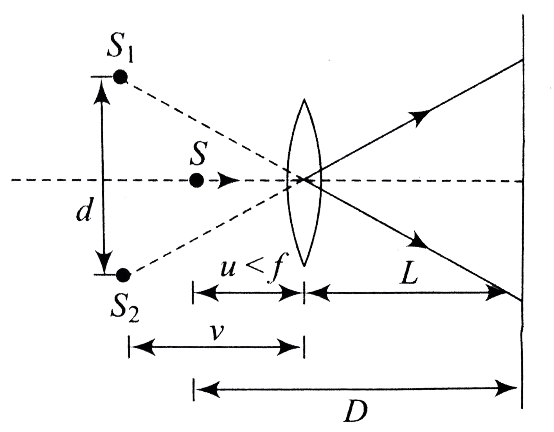

Answer
453k+ views
Hint: We will first calculate the fringe width of the pattern that we will obtain on the screen and use it to calculate the width of maxima under the given condition. After doing that, we calculate the useful height of the screen, that is, the height up to which maximas will form.
It should also be known that after cutting the lens in two halves and joining them, the thickness lost is termed as
Complete answer:
We know, from lens equation:
And, the distance between
Which can also be written as:
Also,
Now, the fringe width can be calculated using the formula:
Putting the value of these terms from above, we get:
On further simplification, we get:
Now, for a condition on Maxima, that is,
Fringe width of maxima:
Now, to calculate the height of screen up to which we obtain a maxima, we use the following diagram:
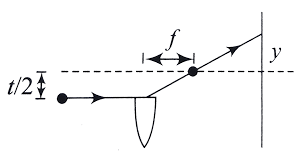
From the above diagram, we can calculate
Therefore, the distance up to which interference occurs (say
Using the value of
Thus, the total number of visible fringes
Hence, the total number of visible fringes is found to be
Hence, option
Note:
These are some very complex problems with very lengthy solutions. While giving a time bound examination like the JEE or NEET, one needs to be very careful as to which questions to pick and solve. Also all the different cases of Double slit, Single slit and interference by lens and mirror should be studied thoroughly as they come under hard concepts of Physics.
It should also be known that after cutting the lens in two halves and joining them, the thickness lost is termed as
Complete answer:
We know, from lens equation:
And, the distance between
Which can also be written as:
Also,
Now, the fringe width can be calculated using the formula:
Putting the value of these terms from above, we get:
On further simplification, we get:
Now, for a condition on Maxima, that is,
Fringe width of maxima:
Now, to calculate the height of screen up to which we obtain a maxima, we use the following diagram:

From the above diagram, we can calculate
Therefore, the distance up to which interference occurs (say
Using the value of
Thus, the total number of visible fringes
Hence, the total number of visible fringes is found to be
Hence, option
Note:
These are some very complex problems with very lengthy solutions. While giving a time bound examination like the JEE or NEET, one needs to be very careful as to which questions to pick and solve. Also all the different cases of Double slit, Single slit and interference by lens and mirror should be studied thoroughly as they come under hard concepts of Physics.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What are the major means of transport Explain each class 12 social science CBSE




