Question

The eye specialist prescribes spectacles of combination of convex lens of focal length 40 cm in contact to a concave lens of focal length of focal length 25 cm. What is the power in diopters?
Option A: +1.5
Option B: -1.5
Option C: 6.67
Option D: -6.67

Answer 1

Hint:The power of lens is the inverse of the focal length of the lens in meters. For a system of lenses the power of the system is known as equivalent power for the system.

Complete solution:
Convex lens:
An optical instrument which is a part of two imaginary spheres, which is transparent and has both the faces bulging outwards, is called a convex lens.
The convex lens converges the rays parallel to its principal axis and incident on it. It has a positive focal length.
So let the focal length of our convex lens be ${f_1}$ and so ${f_1} = + 40cm$

Concave lens:
An optical device that is a part of two imaginary spheres, which is transparent and the faces bulging inside, is called a concave lens.
The concave lens unlike the convex lens diverges the rays’ incident on it and is parallel to the principal axis. The focal length of a concave lens is negative.
So let the focal length of our concave lens be ${f_2}$ and so ${f_2} = - 25cm$.
Power of lens:
The power of a lens is measured in Diopters and is the inverse of its focal length;
$P = \dfrac{1}{f}$
Thus if ${P_1}$ and ${P_2}$ are the powers of the convex and concave lenses respectively then we have,
$$${P_1} = \dfrac{1}{{{f_{ & 1}}}}$ and ${P_2} = \dfrac{1}{{{f_2}}}$ respectively
But here are system is a combination of two systems and so, the equivalent power of the system is given by;
${P_{eq}} = {P_1} + {P_2} - d{P_1}{P_2}$
Here d is the distance between the two lenses.

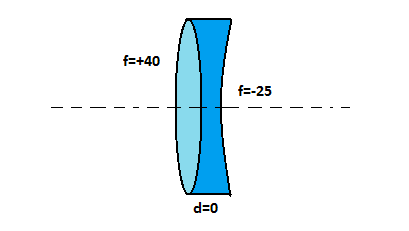
The diagram above will help you understand the situation. As you can see the distance between the two lenses is zero we have d = 0
Hence the equivalent power of the system is given by;
${P_{eq}} = {P_1} + {P_2} - d{P_1}{P_2}$
\[ \Rightarrow {P_{eq}} = {P_1} + {P_2} - 0\]
$ \Rightarrow {P_{eq}} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
Thus, substituting values we get;
$ \Rightarrow {P_{eq}} = \dfrac{{100}}{{ + 40}} + \dfrac{{100}}{{ - 25}}$
$\therefore {P_{eq}} = - 1.5D$

Therefore option B is correct.

Note:
The equivalent focal length of the system can also be calculated.
It is given by ${f_{eq}} = \dfrac{{{f_1}{f_2}}}{{{f_1} + {f_2} - d}}$.
As you can see power decreases with increase in the distance between the lenses.
The above formula is valid for a two lens system, for a system with more lenses try making pairs and solving it with the same approach.