
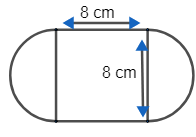
The figure above consists of a square and 2 semicircle, with dimensions as shown. Calculate its outside perimeter (in centimeters)
$\begin{align}
& \text{A}\text{. }8+8\pi \\
& \text{B}\text{. }16+8\pi \\
& \text{C}\text{. }16+16\pi \\
& \text{D}\text{. }32+8\pi \\
& \text{E}\text{. }32+16\pi \\
\end{align}$

Answer
584.7k+ views
Hint: To find the perimeter of the given figure, first we will find the outer surface of the semicircle which is also known as the circumference of a half circle. Then we will find the perimeter of the figure by adding all the sides of the figure.
Complete step by step solution:
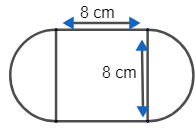
From the figure, we get to know that –
It consists of a square and 2 semicircles and the side of a square is equal to the diameter of the semicircle. i.e. $s=d=8$ …….. (1)
We know that –
$2\text{ Semicircles = Circle}$
Dividing both sides by 2, we get –
$\text{Semicircle=}\dfrac{1}{2}\text{Circle}$ …………………. (2)
We know that the perimeter of a circle is also known as circumference of a circle.
So the circumference of a $\dfrac{1}{2}$ circle $=\dfrac{1}{2}2\pi r$
Where, $r=\dfrac{d}{2}$ and $d=8$ (from equation 1)
So the circumference of a $\dfrac{1}{2}$ circle $=\dfrac{1}{2}\times 2\times \pi \times \dfrac{8}{2}$
By cancelling the common factor from numerator and denominator, we get –
$=4\pi $
Therefore, from equation (2) –
$\text{circumference of }\dfrac{1}{2}\text{ circle = circumference of semicircle =4}\pi $ …………………… (3)
Now, we will find the outside perimeter of the given figure.
The perimeter is the sum of all sides of the figure,
Let us consider, ‘s’ as the sides of squares and ‘c’ is the circumference of the semicircle.
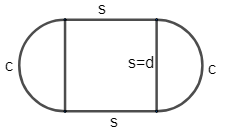
The perimeter of the given figure is $s+c+s+c$ .
By substituting the values from equation 1 and 3, we get that –
$\begin{align}
& 2s+2c=2\left( 8 \right)+2\left( 4\pi \right) \\
& =16+8\pi \\
\end{align}$
Therefore, the perimeter of the given figure is $16+8\pi $ .
Hence, the correct option is B.
Note: To solve this problem students must know that the length of a straight sided shapes outline is called perimeter, and the length of a circle’s outline is called its circumference. Here in this question there are 2 semi circles which is equal to a circle of same dimension
For example:
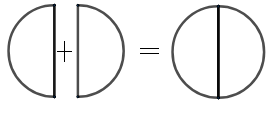
From the figure we can clearly see that the 2 semicircles of the same radius are equal to the circle of the same radius.
So, to find the perimeter of a circle we must need to find the circumference of semicircles.
Complete step by step solution:

From the figure, we get to know that –
It consists of a square and 2 semicircles and the side of a square is equal to the diameter of the semicircle. i.e. $s=d=8$ …….. (1)
We know that –
$2\text{ Semicircles = Circle}$
Dividing both sides by 2, we get –
$\text{Semicircle=}\dfrac{1}{2}\text{Circle}$ …………………. (2)
We know that the perimeter of a circle is also known as circumference of a circle.
So the circumference of a $\dfrac{1}{2}$ circle $=\dfrac{1}{2}2\pi r$
Where, $r=\dfrac{d}{2}$ and $d=8$ (from equation 1)
So the circumference of a $\dfrac{1}{2}$ circle $=\dfrac{1}{2}\times 2\times \pi \times \dfrac{8}{2}$
By cancelling the common factor from numerator and denominator, we get –
$=4\pi $
Therefore, from equation (2) –
$\text{circumference of }\dfrac{1}{2}\text{ circle = circumference of semicircle =4}\pi $ …………………… (3)
Now, we will find the outside perimeter of the given figure.
The perimeter is the sum of all sides of the figure,
Let us consider, ‘s’ as the sides of squares and ‘c’ is the circumference of the semicircle.

The perimeter of the given figure is $s+c+s+c$ .
By substituting the values from equation 1 and 3, we get that –
$\begin{align}
& 2s+2c=2\left( 8 \right)+2\left( 4\pi \right) \\
& =16+8\pi \\
\end{align}$
Therefore, the perimeter of the given figure is $16+8\pi $ .
Hence, the correct option is B.
Note: To solve this problem students must know that the length of a straight sided shapes outline is called perimeter, and the length of a circle’s outline is called its circumference. Here in this question there are 2 semi circles which is equal to a circle of same dimension
For example:
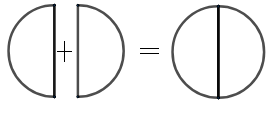
From the figure we can clearly see that the 2 semicircles of the same radius are equal to the circle of the same radius.
So, to find the perimeter of a circle we must need to find the circumference of semicircles.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




