Question

The figure below shows a square ABCD of side 6 cm. Given that E is the midpoint of AB, points F and G are on BC so that BF = FG = GC. What is the total area of the shaded region in $c{{m}^{2}}?$

Answer 1

Hint: This type of question can be solved by using the concept of congruence of triangles. We divide the square into the necessary number of triangles, and using the property of congruence, we find out what the area of each of the portions is and we finally calculate what the area of the shaded region is.

Complete step by step solution:
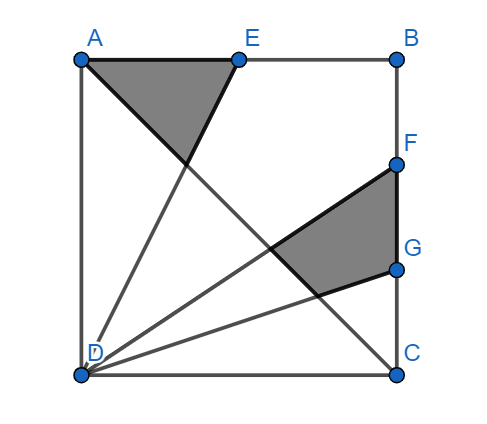
Question given shows 2 regions shaded and we are required to calculate the total area of these shaded regions. Let us analyse this figure and draw the necessary figures as shown.
Fig1

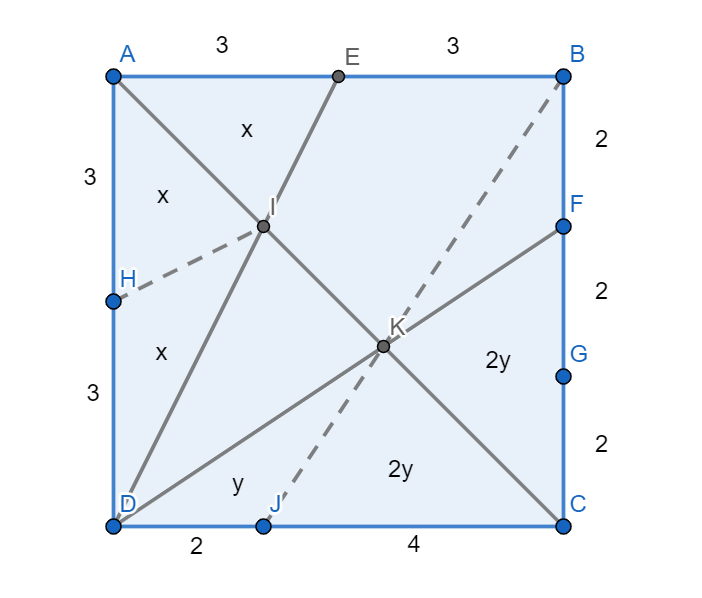
Fig2

From fig1, as we know that E is the midpoint of side AB we know the length of the segment AE is 3 cm. We now divide the side DA into two equal halves with a midpoint at H. We connect this point to the intersection point of line segments AC and ED which is labelled as I.
Similarly, we choose point J on the side CD as such that it divides the line into a ratio of 2:1. We then connect this point to the point B.
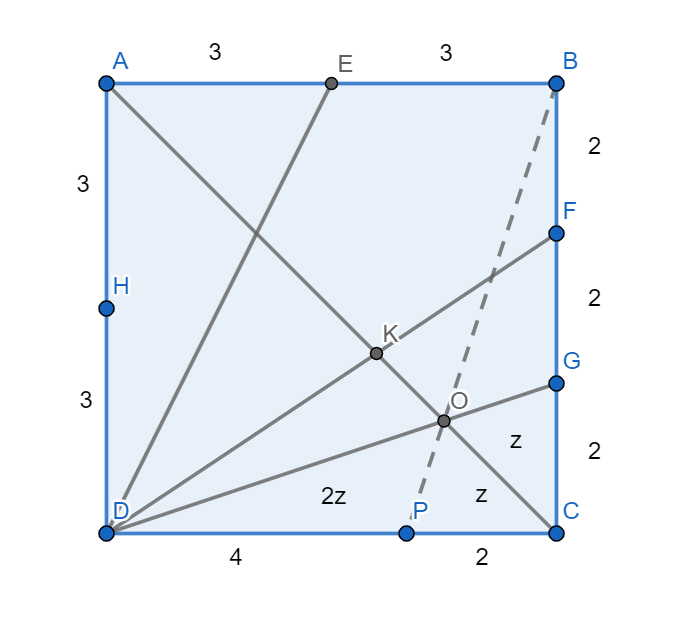
From fig2, we choose point P on the side CD as such that it divides the line into a ratio of 1:2. We then connect this point to the point B.
From the 2 figures, we can see that the total area shaded is given by $A=x+2y-z......\left( 1 \right),$ where x, y and z are the regions as indicated by the figures.
Refer to figure 1,
We are required to find x now. We can see that the $\Delta EIA$ and $\Delta HIA$ are congruent (common side).
Let their areas $Area\left( \Delta EIA \right)=Area\left( \Delta HIA \right)=x,$
$\Rightarrow Area\left( \Delta DIH \right)=x$
We know that the area of a right-angled triangle is given by $Area=\dfrac{1}{2}\times base\times height.$
Therefore,
$\Rightarrow Area(\Delta DAE)=\dfrac{1}{2}\times 3\times 6$
$\Rightarrow Area(\Delta DAE)=9c{{m}^{2}}$
Therefore, area x is nothing but one-third of this $Area(\Delta DAE)$ ,
$\Rightarrow x=\dfrac{1}{3}\times 9c{{m}^{2}}$
$\Rightarrow x=3c{{m}^{2}}$
We are required to find y now. Let the $Area\left( \Delta DKJ \right)=y.$
$\Rightarrow Area\left( \Delta JKC \right)=2y$
We can see that $\Delta JKC$ and $\Delta CKF$ are congruent (common side).
$\Rightarrow Area\left( \Delta JKC \right)=Area\left( \Delta CKF \right)=2y$
We now calculate the area of the $\Delta DCF.$
$\Rightarrow Area(\Delta DCF)=\dfrac{1}{2}\times 4\times 6$
$\Rightarrow Area(\Delta DCF)=12c{{m}^{2}}$
As we can see, the sum of all the areas inside is equal to the total area,
$\Rightarrow y+2y+2y=12c{{m}^{2}}$
$\Rightarrow 5y=12c{{m}^{2}}$
Therefore, we get y as,
$\Rightarrow y=\dfrac{12}{5}c{{m}^{2}}=2.4c{{m}^{2}}$
Refer to figure 2 now,
We are required to find z now. We can see that the $\Delta GOC$ and $\Delta COP$ are congruent (common side).
Let their areas $Area\left( \Delta GOC \right)=Area\left( \Delta COP \right)=z.$
$\Rightarrow Area\left( \Delta POD \right)=2z$
We now calculate the area of the $\Delta DCG.$
$\Rightarrow Area(\Delta DCG)=\dfrac{1}{2}\times 2\times 6$
$\Rightarrow Area(\Delta DCG)=6c{{m}^{2}}$
As we can see, the sum of all the areas inside is equal to the total area,
$\Rightarrow z+z+2z=6c{{m}^{2}}$
$\Rightarrow 4z=6c{{m}^{2}}$
Therefore, we get z as,
$\Rightarrow z=\dfrac{6}{4}c{{m}^{2}}=1.5c{{m}^{2}}$
From $A=x+2y-z,$ we get the area of the shaded region.
$\Rightarrow A=3+2\times 2.4-1.5$
$\Rightarrow A=6.3c{{m}^{2}}$
Hence the area of the shaded region is $6.3c{{m}^{2}}.$

Note: To solve this question, students are required to have a good knowledge in the topic of congruence of triangles and care must be taken while drawing the diagram during solution and we should draw only the required number of lines in order to get the solution. Unnecessary lines can complicate the diagram and make it difficult for the student to identify the required areas.