Question

The figure below shows regular hexagons, with charges at the vertices. In which of the following cases the electric field at the center is not zero.

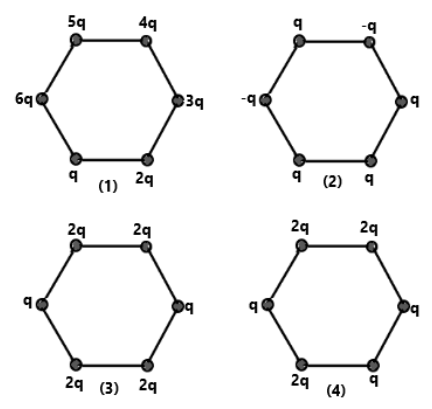
A) $4$
B) $3$
C) $1$
D) $2$

Answer 1

Hint: At the center of every hexagon, the electric field is zero. Here, the electric field will be zero because the charges of the same values with opposite charges will terminate each other i.e. $$\text{ + q}$$ and $$\text{ - q}$$ in each corner cancel out each other.

Complete step by step answer:
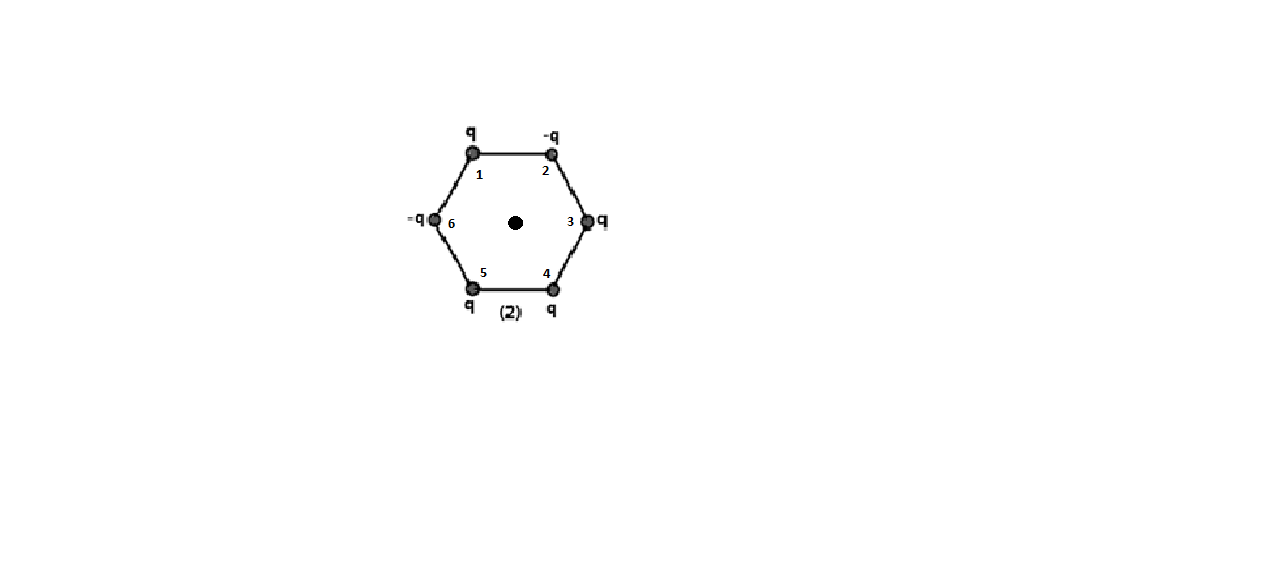
The charge at the position $1$ and the charge at the position $4$ cancel each other.
Whereas, the charges at positions $2$ , $5$ , and $3$ , $6$ will not cancel each other.


The magnitude of the electric field $$\left(E\right)$$occurred by a point charge with a charge of magnitude $$Q$$ , at some distance $r$ away from the point charge, is given by the equation $$E={\displaystyle \frac{k\text{Q}}{r^2}}$$.
Where $$k=8.99\times {10}^9\text{ N }{\displaystyle \frac{{\text{m}}^2}{c^2}}$$.

Hence, the right answer is in option $(D)\Rightarrow 2$ .

Additional information:
The electric field is outlined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it might exert on a positive test charge. The electric field is radially outward from a positive charge and in toward a negative charge.

Note: Electric fields allow all things electrical to operate from the simple flashlight to the light switch you turn on when you enter a room and all the way on up to every single device using any form of electricity or Electronics including every computer, smartphone, radio, television, auto, airplane, and many medical advances.