Question

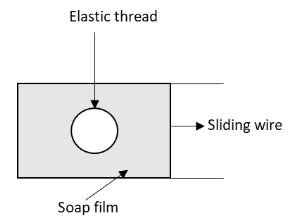
The figure shows a soap film in which a closed elastic thread is lying. The film inside the thread is priced. Now the sliding wire is moved out so that the surface area increases.The radius of the circle formed by the elastic thread will:

A. increases
B. decreases
C. remains same
D. data insufficient

Answer 1

Hint:Use the formula for tension force acting on an object. This formula gives the relation between the tension force, the force acting on the object and the length on which the force is acting. Check whether the resultant force on the closed thread is balanced or not and length of the elastic thread increases or not. Hence, using this formula check whether the tension force remains the same or not which will give an idea about the radius of the circle formed by the closed thread.

Formula used:
The formula for surface tension \[T\] is given by
\[T = \dfrac{F}{l}\] …… (1)
Here, \[F\] is the force acting and \[l\] is the length of which the force is acting.

Complete answer:
We have given that a closed elastic thread is lying on a soap film. The soap film inside the elastic thread is pricked and the sliding wire is moved out in order to increase the area of the soap film.We have asked the effect of increasing the area of the soap film and pricking the soap film inside the closed thread on the radius of the closed thread.From equation (1), we can conclude that the tension force depends only on the force exerted and length on which force is acting.

For the closed elastic thread lying inside the soap film, before pricking off the soap film and sliding the wire out, the net resultant force acting on the closed thread is zero. Hence, the thread is stable on the soap film.When the sliding wire is moved in the outward direction, the area of the soap film increases. Also the soap film inside the closed thread is pricked, so now there is no soap film inside the closed thread.

But from equation (1), we can conclude that the tension force depends on length of the closed thread and the length of the closed thread remains the same when the soap film is pricked as there is no resultant external force causing the length of the thread to increases.Since, the tension force on the closed thread is balanced, the area and hence, the radius of the circle remains the same.

Hence, the correct option is C.

Note:The students may think that as the closed thread is elastic and pricking the soap film inside the thread, the net tension force of the soap film on the thread is outward which should increase the radius of the closed thread. But the students should keep in mind that this tension force on thread is the same from all sides. Thus, the net force becomes zero and the radius of the closed thread remains the same.