Question

The figure shows a sphere of radius r that carries a total charge Q uniformly distributed throughout its volume.
Which of the following expressions gives the electric field strength at point P, a point that lies inside the sphere and is a distance r from the center of the sphere?

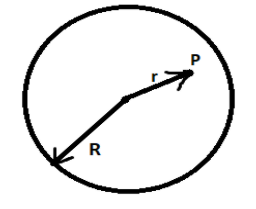
A) $E = \dfrac{{Qr}}{{4\pi {\varepsilon _0}{R^3}}}$
B) $E = \dfrac{Q}{{4\pi {\varepsilon _0}{r^2}}}$
C) $E = 0$ (Point P is inside of conductor)
D) $E = \dfrac{{3Qr}}{{4\pi {\varepsilon _0}{R^3}}}$

Answer 1

Hint: We can consider a Gaussian surface for point P and distance from center become radius for this surface. We can use the following relationship to calculate electric strength at point P.
$\phi = E\iint {da}$ where $\phi $ and E is electric flux and field respectively and $\iint {da}$ is surface integral or area of the body.
$\phi = \dfrac{q}{{{\varepsilon _0}}}$ where q is the charge.
Volume charge density of a Gaussian surface is :
\[\dfrac{{Charge{\text{ }}in{\text{ }}body}}{{Volume{\text{ }}of{\text{ }}body}} \times Volume{\text{ }}of{\text{ }}Gaussian{\text{ }}surface{\text{ }}\].

Formula used:
Area of sphere = $4\pi {r^2}$
Volume of sphere = $\dfrac{4}{3}\pi {r^2}$

Complete step by step answer:
Drawing a Gaussian surface around point P to get the electric flux:

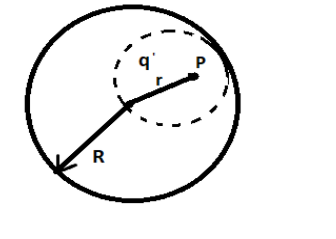
Let charge be enclosed in this Gaussian surface. Then according to Gaussian theorem, the flux inside this surface is given as:
$\phi = E\iint {da}$
For a square, the area will be $4\pi {r^2}$ so:
$\iint {da} = 4\pi {r^2}$ [r being distance from center for P]
$ \Rightarrow \phi = E \times 4\pi {r^2}$ ……… (1)
According to Gauss’ s law, the electric flux is equal to $\dfrac{1}{{{\varepsilon _0}}}$ times the charge contained.
The charge contained in the Gaussian surface is, so:
$\phi = \dfrac{{q'}}{{{\varepsilon _0}}}$ ………….. (2)
As both (1) and (2) represent electric fields for the Gaussian surface, they will be equal.
$\Rightarrow E \times 4\pi {r^2} = \dfrac{{q'}}{{{\varepsilon _0}}} \\$
 $ \implies E = \dfrac{{q'}}{{4\pi {r^2}{\varepsilon _0}}}......(3) \\ $
Now, the charge enclosed by this Gaussian surface is the volume charge density of the sphere.
Volume of sphere is $\dfrac{4}{3}\pi {r^3}$ and the charge contained in the sphere is Q, so:
$q' = \dfrac{Q}{{\dfrac{4}{3}\pi {R^3}}} \times \dfrac{4}{3}\pi {r^3} \\$
$ q' = Q\dfrac{{{r^3}}}{{{R^3}}} \\ $ [r is radius of Gaussian surface and R is radius of the sphere]
Substituting this value in (3), we get:
$ E = \dfrac{1}{{4\pi {\varepsilon _0}{r^2}}} \times Q\dfrac{{{r^3}}}{{{R^3}}} \\$
$E = \dfrac{{Qr}}{{4\pi {\varepsilon _0}{R^3}}} \\ $
Therefore, the electric field strength at point P, that lies inside the sphere at distance r from the center of the sphere is \[E = \dfrac{{Qr}}{{4\pi {\varepsilon _0}{R^3}}}\] and the correct option is A).

So, the correct answer is “Option A”.

Note:
The Gaussian surface is basically a 3-D space to calculate flux of electric fields.
Electric field in general terms is the rate of flow of electric field lines flowing in/out the given surface.
Flux can be produced on the spherical Gaussian surface due to a point charge, or shell with uniform charge distribution or symmetrical charge distribution.