Question

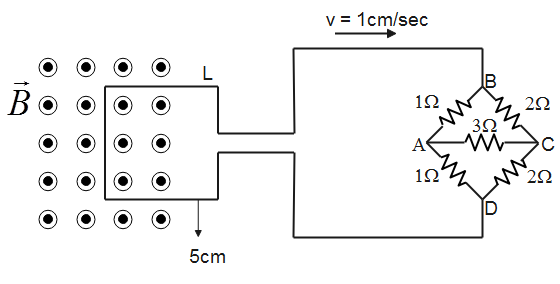
The figure shows a square loop L of side $5cm$ which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of $1\,cm{{s}^{-1}}$. At some instant, a part of L is in a uniform magnetic field of $1T$, perpendicular to the plane of the loop. If the resistance of L is $1.7\Omega $, what will be the approximate current in the loop at that instant?

A. $115\mu A$
B. $170\mu A$
C. $60\mu A$
D. $150\mu A$

Answer 1

Hint: First, calculate the total resistance of the loop. The network of resistors appears to be a Wheatstone bridge. Varying magnetic flux through the loop induced emf. Use the expression of motional emf to find the emf induced. The motional emf is equivalent to voltage across the circuit. Use Ohm’s law to obtain electric current in the loop.

Formula used:
Ohm’s law, $V=IR$

Complete step by step answer:
First, we shall calculate the resistance of the loop. We can note that the resistances between B and D are in Wheatstone bridge form as
$\dfrac{{{R}_{BA}}}{{{R}_{AD}}}=\dfrac{{{R}_{BC}}}{{{R}_{CD}}}$
Therefore, the $3\Omega $ resistance can be neglected as no current flows through it.
Now the circuit becomes as shown below.

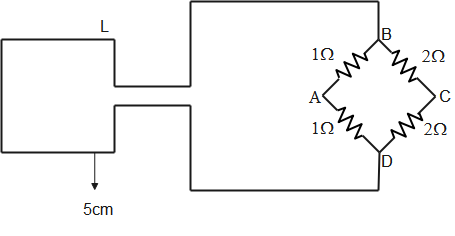
The resistances ${{R}_{BA}}$ and ${{R}_{AD}}$; and ${{R}_{CA}}$ and ${{R}_{CD}}$ are in series and therefore can be replaced with single resistance equivalent to sum of their resistances. Now the circuit can be redrawn as shown below.

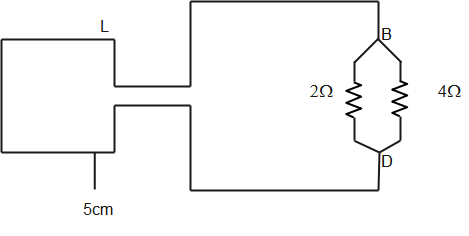
We can note that, the $2\Omega $ and $4\Omega $ are in parallel and their equivalent resistance is given by
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}$
$\Rightarrow {{R}_{eq}}=\dfrac{4}{3}\Omega \approx 1.3\Omega $
Given that the resistance of L is $1.7\Omega $. Therefore, net resistance through the loop is ${{R}_{loop}}=1.7+1.3\approx 3\Omega $
Emf induced in a loop with its area vector along magnetic field and moving perpendicular to the magnetic field is given by
$\epsilon=Blv$
Where b is the magnetic field and $l$ is the length which is perpendicular to motion of the loop.

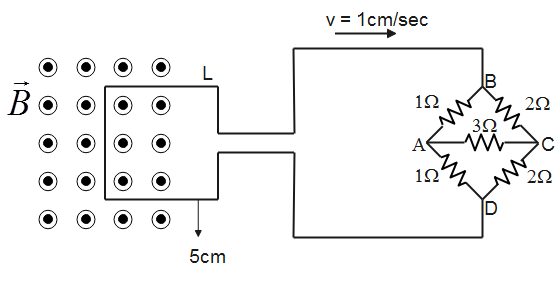
Substituting the values, we have
$\epsilon =1T\times 5cm\times 1cm/s=5\times {{10}^{-4}}T{{m}^{2}}/s$
Current through the loop,
$I=\dfrac{\epsilon }{{{R}_{loop}}}=\dfrac{5\times {{10}^{-4}}V}{3\Omega }=1.67\times {{10}^{-4}}A\approx 170\mu A$
Therefore, option B is correct.

Note:
Varying magnetic field induces electric current and therefore induces electric field. If magnetic flux through the loop is not changing, induced current will be zero.
Some basic conversions are often required in numerical problems. So, learn about milli-, centi-, micro-, kilo- etc.