Question

The figure shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be $45\;cm$. The liquid is removed and the experiment is repeated. The new distance is measured to be $30\;cm$. What is the refractive index of the liquid?

Answer 1

Hint: Try and understand the possible relationship between the distance(s) of the needle from the lens and the focal length of the lens. The next thing to do ahead would be to deduce the focal length of the liquid layer from the effective focal length. Once this is done find the radius of curvature of the lens, and then in addition with the refractive index of the liquid and its radii of curvature on both sides, you can consequently find the refractive index of the liquid layer.

Formula used:
Equivalent focal length F: $\dfrac{1}{F} = \dfrac{1}{f_1} +\dfrac{1}{f_2}$, where $f_1$ and $f_2$ are the focal lengths of the two optical bodies in contact.
Lens maker’s formula:
Focal length f: $\dfrac{1}{f} = \left(\mu -1\right) \left(\dfrac{1}{R_1} -\dfrac{1}{R_2} \right)$, where $\mu$ is the refractive index, $R_1$ is the radius of curvature of the surface close to the object, and, $R_2$ is the radius of curvature of the surface farther away from the object.


Complete step by step answer:
Let us try and understand what we have to work with.
We have two cases: one with the liquid layer and one without the liquid layer between the mirror and the lens.
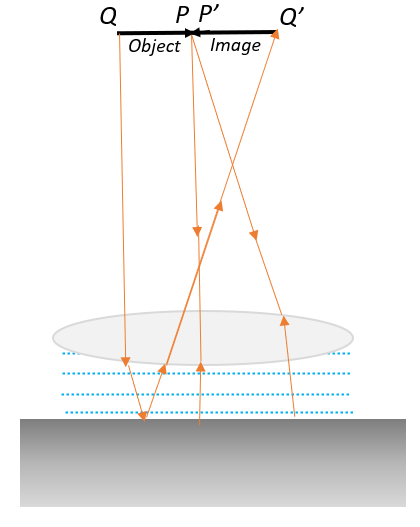
When there is no liquid layer, the only refracting medium is the convex lens. If the needle is oriented as PQ on the principal focus, the rays from P pass through the lens un-deviated (since the P-end of the needle is on the principal axis which passes through the optical centre of the lens) and gets inverted back to the axis as a result of being reflected back from the mirror.
As for the rays from end Q, we can back-track their path for an easier understanding. Since they form an inverted image after reflection and subsequent convergence, this can only mean that they were parallel rays before convergence, which would then mean that the rays emerging from the object had to be from the focal point, since parallel rays are formed with a convex lens only when the object is at the focus.
Therefore, we can establish that when there is no liquid layer, the object and the image are formed at the focus. This means that the focal length of the lens is $f_{lens} = 30\;cm$
When there is a liquid layer, the same above principle applies but instead we get a combined focal length of the liquid layer and the convex lens. Therefore, $f_{equivalent} = 45\;cm$
For a pair of optical instruments in contact, the equivalent focal length is given as
$\dfrac{1}{f} = \dfrac{1}{f_1} +\dfrac{1}{f_2}$
In our case this would look like:
$\dfrac{1}{f_{equivalent}} = \dfrac{1}{f_{lens}} +\dfrac{1}{f_{liquid}} \Rightarrow \dfrac{1}{f_{liquid}} = \dfrac{1}{f_{equivalent}} -\dfrac{1}{f_{lens}} $
$\Rightarrow \dfrac{1}{f_{liquid}} = \dfrac{1}{45} - \dfrac{1}{30} = -\;\dfrac{1}{90} \Rightarrow f_{liquid} = -\;90\;cm$
Now, let the radius of curvature of the lens on the object-side be $R \Rightarrow$ the radius of curvature of the lens on the other side, i.e., the side in contact with the liquid layer be $-\;R$. Note that thus, $-\;R$ will also be the radius of curvature of the liquid layer in contact with the lens. The radius of curvature of the liquid layer in contact with the plane mirror will be $\infty$.
First, let us consider the lens w.r.t the object ($R_1$ is convexly shaped, $R_2$ is concavely shaped).
The radius of curvature R can be obtained using the relation:
$\dfrac{1}{f_{lens}} = \left(\mu_{lens} -1\right) \left(\dfrac{1}{R} +\dfrac{1}{-R} \right) \Rightarrow \dfrac{1}{30} = \left(0.15 -1\right) \left(\dfrac{2}{R}\right) \Rightarrow R = \dfrac{30}{0.5 \times 2} = 30\;cm$
Now let us consider the liquid layer w.r.t the object ($R_1$ is concavely shaped and $R_2$ is flat)
Using the same relation as above, we can find $\mu_{liquid}$ instead:
$\dfrac{1}{f_{liquid}} = \left(\mu_{liquid} -1\right) \left(\dfrac{1}{-R} -\dfrac{1}{\infty} \right) \Rightarrow \dfrac{1}{-90} = \left(\mu_{liquid} -1\right) \left(\dfrac{1}{30} - 0 \right) \Rightarrow \mu_{liquid} = \dfrac{1}{3} +1 = \dfrac{4}{3} = 1.33$
Therefore, the refractive index of the liquid layer is $\mu_{liquid} = 1.33$

Note:
The sign convention used for the radii of curvature is $R_1$ is positive for a convex lens but negative for a concave lens, and $R_2$ is negative for a convex lens and positive for a concave lens.
Also remember that the radius of curvature of a flat surface is $\infty$ since it does curve at any point.