Question

The figure shows an RC circuit with a parallel plate capacitor. Before switching on the circuit, plate A of the capacitor has a charge $ -Q_{0} $ while plate $ \mathrm{B} $ has no net charge. Now, at $ t=0, $ the circuit is switched on. How much time (in second) will elapse before the net charge on plate A becomes zero?

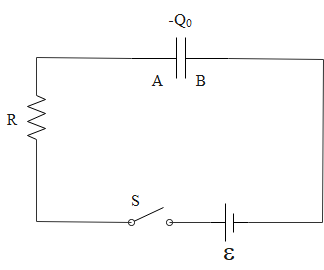
(Given $ C=1 \mu F, Q_{0}=1 \mathrm{m} C, \mathcal{E}=1000 \mathrm{V} $ and $ \left.R=\dfrac{2 \times 10^{6}}{\ln 3} \Omega\right) $
(A) 2
(B) 3.33
(C) 1.33
(D) 1.67

Answer 1

Hint
We should know that an RC circuit is a circuit with both a resistor or R and a capacitor or C. RC circuits are frequent elements in electronic devices. They also play an important role in the transmission of electrical signals in nerve cells. The RC circuit is used in camera flashes, pacemaker, timing circuit etc. The RC signal filters the signals by blocking some frequencies and allowing others to pass through it. It is also called first-order RC circuit and is used to filter the signals bypassing some frequencies and blocking others. It is required to use this concept to solve this question.

Complete step by step answer
We know that,
At any time $ t_{0} $ after $ t=0 $
Let $ q=Q_{0} $ at $ t=t_{0} $
 $ \therefore \mathrm{Q}_{+}=0 $
 $ \Rightarrow \mathrm{V}_{\text {capacitor }}=\dfrac{\mathrm{Q}_{+}-\mathrm{Q}_{-}}{2 \mathrm{C}} $ (Capacitance)
 $ \therefore $ By KVL
 $ \Rightarrow \mathrm{E}-\dfrac{\mathrm{d} \mathrm{q}}{\mathrm{dt}} \mathrm{R}-\dfrac{\left(\left(-\mathrm{Q}_{0}+\mathrm{q}\right)-(-\mathrm{q})\right)}{2 \mathrm{C}_{\mathrm{AB}}}=0 $
 $ \Rightarrow \mathrm{E}-\dfrac{2 \times 10^{6}}{\ln 3} \dfrac{\mathrm{dq}}{\mathrm{dt}}-\left[\dfrac{-\mathrm{Q}_{0}+2 \mathrm{q}}{2 \times 1 \times 10^{-6}}\right]=0 $
By substituting given values
$ \therefore\left[1000+\dfrac{10^{-3}}{2 \times 10^{-6}}\right]-\dfrac{2 \times 10^{6}}{\ln 3} \dfrac{\mathrm{dq}}{\mathrm{dt}}-\dfrac{\mathrm{q}}{10^{-6}}=0 $
 $ \therefore 1500-\dfrac{2 \times 10^{6}}{\ln 3} \dfrac{\mathrm{dq}}{\mathrm{dt}}-\dfrac{\mathrm{q}}{10^{-6}}=0 $
 $ \therefore \dfrac{\mathrm{dq}}{\mathrm{dt}}=\left[\dfrac{1500 \times 10^{-6}-\mathrm{q}}{2}\right] \ln 3 $
 $ \therefore \int_{0}^{\mathrm{Q}_{0}} \dfrac{\operatorname{dq}(1 \times 2)}{\left(1500 \times 10^{-6}-9\right) \ln 3}=\int_{0}^{t_{0}} \mathrm{dt} $
 $ \Rightarrow \int_{0}^{10^{-3}} \dfrac{\operatorname{dq}(2)}{\left(1500 \times 10^{-6}-\mathrm{q}\right) \ln 3}=\mathrm{t}_{0}=2.19 \mathrm{sec} \simeq 2 $ .
Therefore, the correct answer is Option (A).

Note
It is required to know the meaning of the concepts of the terms that are used in the answer. So, as it is known that a capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals. The effect of a capacitor is known as capacitance. A capacitor works on the principle that the capacitance of a conductor increases appreciably when an earthed conductor is brought near it. Hence, a capacitor has two plates separated by a distance having equal and opposite charges.
It should be known to us that the most common kinds of capacitors are: Ceramic capacitors have a ceramic dielectric. Film and paper capacitors are named for their dielectrics. Aluminium, tantalum and niobium electrolytic capacitors are named after the material used as the anode and the construction of the cathode which is used as an electrolyte.