Question

The following are rectangles.
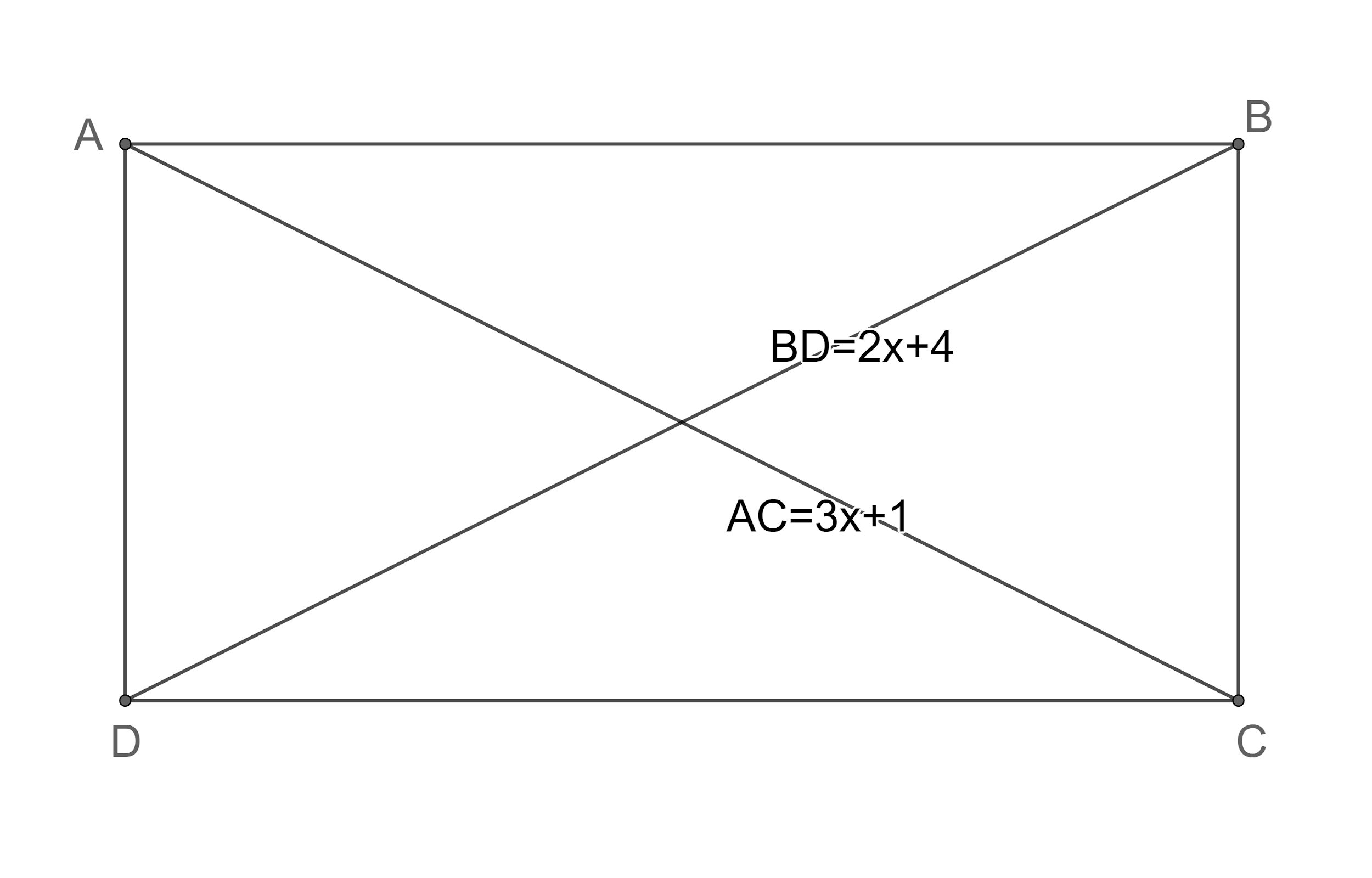
(i) If the length of the diagonals AC and BD of the rectangle ABCD are given as $2x+4$ and $3x+1$ (as shown in figure below). Find the length of the diagonals.

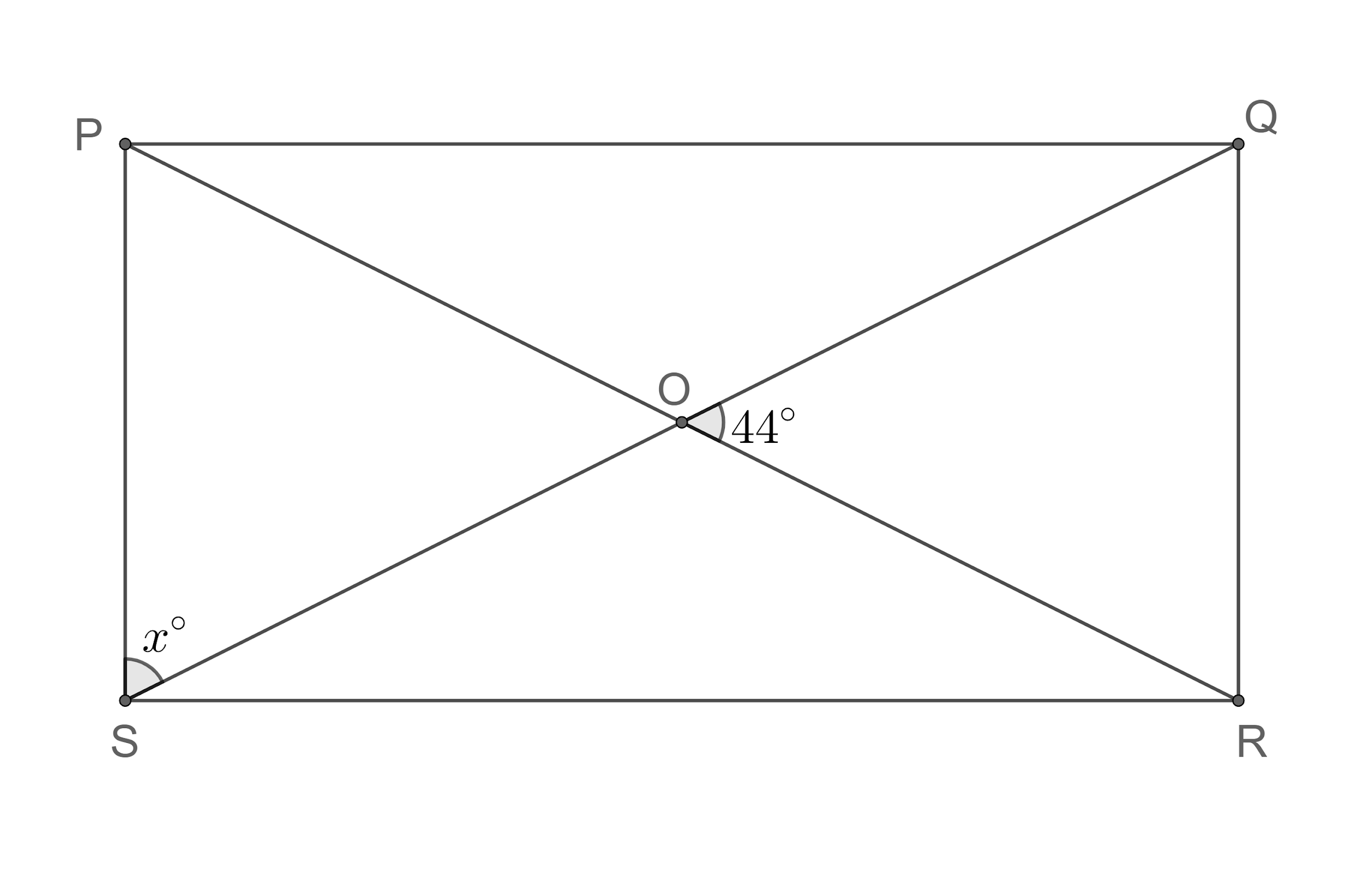
(ii) If O is the point of the intersection of diagonals PR and QS in rectangle PQRS and angle $\angle QOR$ is equal to ${{44}^{\circ }}$, then find the value of angle ${{x}^{\circ }}$ as shown in figure?

Answer 1

Hint: We start solving the problem (i) by using the fact that lengths of the diagonal in a rectangle are equal. We equate the given lengths of diagonals to find the value of ‘x’ using which we find the lengths of the diagonals. We then start solving the problem (ii) by using the fact that vertically opposite angles and also the fact that the lengths of the diagonals in a rectangle are equal and they bisect each other at their intersection point. We then use the fact that angles opposite to the equal sides are equal and sum of the angles in a triangle is ${{180}^{\circ }}$ to find the value of angle ‘x’.

Complete step-by-step answer:
(i) According to the problem, we are given the length of the diagonals AC and BD of the rectangle ABCD are given as $2x+4$ and $3x+1$. We need to find the length of the diagonal.
Let us redraw the figure of the rectangle ABCD.

We know that the lengths of the diagonals in a rectangle are equal.
So, we have $3x+1=2x+4$.
$\Rightarrow x=3$.
Let us substitute this in the given length to find the lengths of diagonals.
So, we get $2x+4=2\left( 3 \right)+4=10$ and $3x+1=3\left( 3 \right)+1=10$.
∴ The length of the diagonal of the rectangle ABCD is 10 units.

(ii) According to the problem, we are given that O is the point of the intersection of diagonals PR and QS in rectangle PQRS and angle $\angle QOR$ is equal to ${{44}^{\circ }}$ and we need to find the value of ${{x}^{\circ }}$ which is as shown in figure.

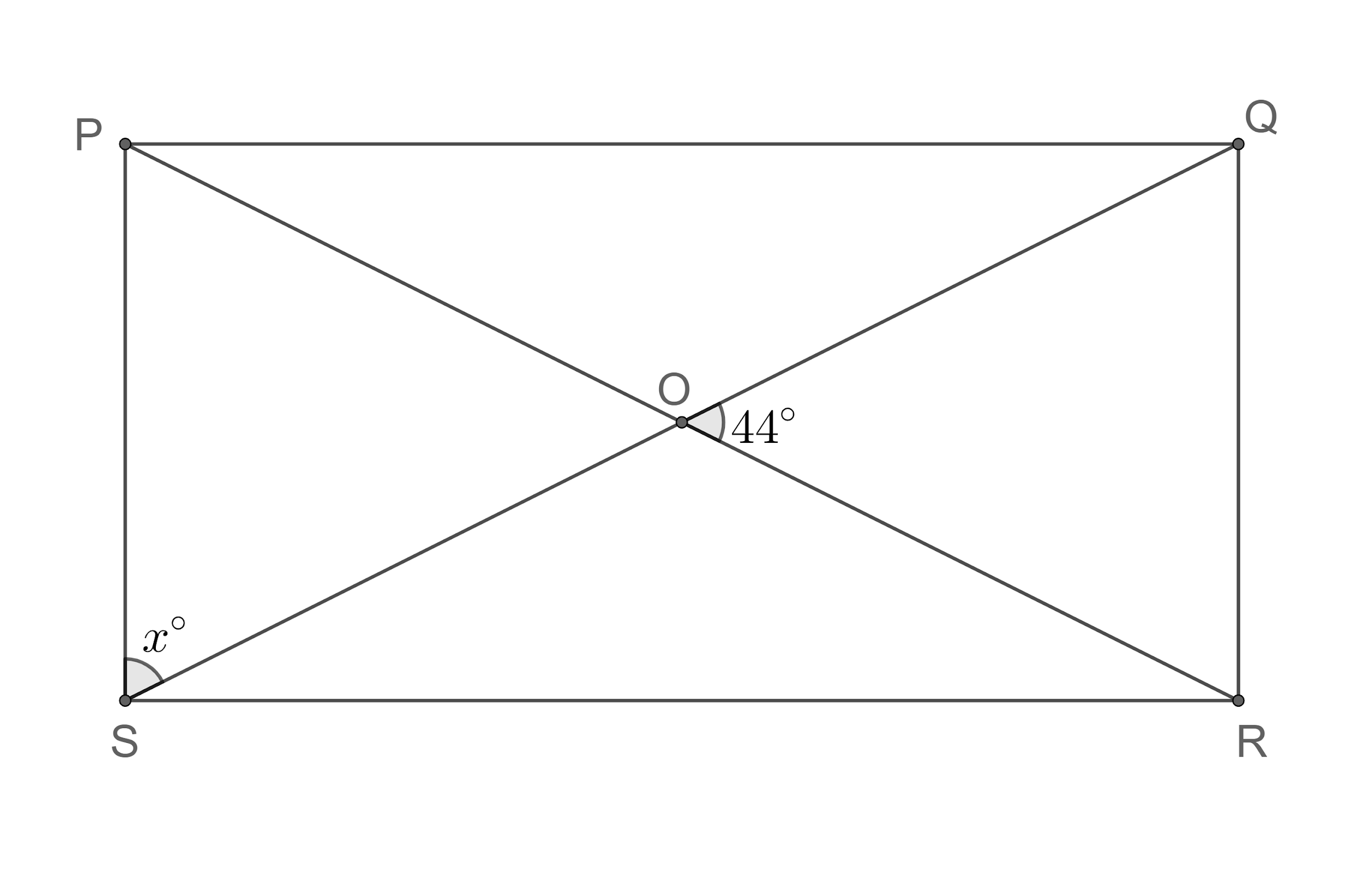
From the figure, we can see that the angles $\angle QOR$ and $\angle POS$are vertically opposite angles.
So, we get $\angle QOR=\angle POS={{44}^{\circ }}$ ---(1).
We know that the lengths of the diagonals in a rectangle are equal and they bisect each other.
So, we get $PO=OS$ ---(2).
We know that the sum of the angles in the triangle $\Delta POS$ is ${{180}^{\circ }}$.
So, we get $\angle OSP+\angle POS+\angle SPO={{180}^{\circ }}$.
From equation (2), we get
$\Rightarrow \angle OSP+{{44}^{\circ }}+\angle SPO={{180}^{\circ }}$ ---(3).
We know that the angles opposite to the equal sides in a triangle are equal. So, we get $\angle OSP=\angle SPO$ as they are opposite to equal sides PO and OS (from equation (2)). We substitute these results in equation (3).
$\Rightarrow \angle OSP+{{44}^{\circ }}+\angle OSP={{180}^{\circ }}$.
$\Rightarrow 2\angle OSP={{136}^{\circ }}$.
$\Rightarrow \angle OSP={{68}^{\circ }}$.
$\Rightarrow x={{68}^{\circ }}$.
We have found the value of ‘x’ as ${{68}^{\circ }}$.

Note: We should not confuse or make calculation mistakes while solving this problem. We should not think that diagonal is the angular bisector of the angles at the vertex in a triangle which is the mistake that most of us commonly do. We need to make sure that we know about the properties of triangles and rectangles properly before solving this problem. Similarly, we can expect problems to find all the angles present in the rectangles by giving one of the sides of the rectangle.