
The force between two charges placed in air resistance at a distance r apart is F. Then the force between the same two charged if a dielectric having k=4 and thickness
A.
B.
C.
D.
Answer
494.7k+ views
Hint: Using Coulomb’s law, find the expression for the force between the two charges for the first case. As for the second case where a dielectric is introduced, remember that the dielectric constant is nothing but the relative permittivity of the material. Use this to get the permittivity of the dielectric in terms of permittivity of free space.
Then, determine the effective distance between the two charges with the dielectric introduced and account for the apparent change in the distance over which the dielectric is placed. Then, using Coulomb’s law, find the effective force between the two charges and arrive at an expression in terms of the force experienced by the charges in the first case.
Formula used: Electric force between two charges:
where
Complete step by step answer:
From Coulomb’s law we know that the electric force between two charges is directly proportional to the product of the magnitude of charges and inversely proportional to the square of the effective distance between them and is given by:
Now, when the two charges are placed in air resistance at a distance r apart, the force between the two charges is given as:
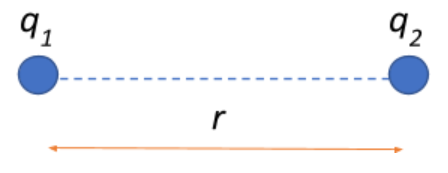
Now, a dielectric of thickness
This means that the electric permittivity of the dielectric is
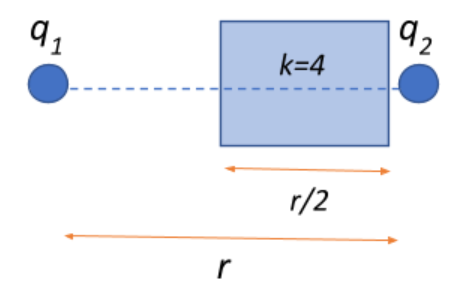
Now, the force acting on the charges due to just the dielectric k can be given in general as:
Thus, when a dielectric is introduced, it has an effect on the distance between the two charges, wherein if r is the actual distance over which the dielectric is introduced, then it behaves as if the distance that the dielectric occupies is
Therefore, the effective distance between the two charges in our arrangement becomes
And the effective force acting between the two charges is given by:
So, the correct answer is “Option A”.
Note: Remember that the apparent change in the actual distance over which the dielectric is introduced is a property of the material that is used as the dielectric. This happens because of the value of the dielectric constant, which gives the relative electrical permittivity of the dielectric material. Note that this apparent change in distance occurs only over the distance between the charges where the dielectric is introduced. The rest of the distance behaves as it was in free space.
Then, determine the effective distance between the two charges with the dielectric introduced and account for the apparent change in the distance over which the dielectric is placed. Then, using Coulomb’s law, find the effective force between the two charges and arrive at an expression in terms of the force experienced by the charges in the first case.
Formula used: Electric force between two charges:
where
Complete step by step answer:
From Coulomb’s law we know that the electric force between two charges is directly proportional to the product of the magnitude of charges and inversely proportional to the square of the effective distance between them and is given by:
Now, when the two charges are placed in air resistance at a distance r apart, the force between the two charges is given as:

Now, a dielectric of thickness
This means that the electric permittivity of the dielectric is

Now, the force acting on the charges due to just the dielectric k can be given in general as:
Thus, when a dielectric is introduced, it has an effect on the distance between the two charges, wherein if r is the actual distance over which the dielectric is introduced, then it behaves as if the distance that the dielectric occupies is
Therefore, the effective distance between the two charges in our arrangement becomes
And the effective force acting between the two charges is given by:
So, the correct answer is “Option A”.
Note: Remember that the apparent change in the actual distance over which the dielectric is introduced is a property of the material that is used as the dielectric. This happens because of the value of the dielectric constant, which gives the relative electrical permittivity of the dielectric material. Note that this apparent change in distance occurs only over the distance between the charges where the dielectric is introduced. The rest of the distance behaves as it was in free space.
Recently Updated Pages
Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the difference between resemblance and sem class 12 social science CBSE




