
The force of interaction of two dipoles, if the two dipoles are parallel to each other and placed at distance x apart.
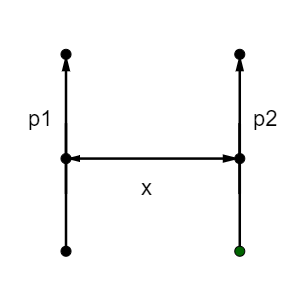
1. \[\dfrac{{3{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
2. \[\dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
3. \[\dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
4. \[\dfrac{{{p_1}{p_2}}}{{3\pi {\varepsilon _ \circ }{x^4}}}\]
Answer
218.7k+ views
Hint: First, we will need to find the electrostatic field of dipole \[{p_2}\] at \[{p_1}\] . Then we will find the potential energy of two dipoles. In the final step we will differentiate the potential energy to get the Force of interaction between two dipoles.
Complete step-by-step Solution
A dipole is separation of two opposite charges and it is quantified by electric dipole moment and is denoted by p.
As we know electric field of dipole along perpendicular bisector of the axis,
\[\overrightarrow E = - \dfrac{{\overrightarrow p }}{{4\pi {\varepsilon _ \circ }{r^3}}}\] , where r= distance
\[{\varepsilon _ \circ }\] = permittivity of free space
\[{E_{21}}\] is the field due to dipole \[{p_1}\] at dipole \[{p_2}\]
\[{E_{21}} = \dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Potential energy of dipole system
\[U = - \overrightarrow {{p_2}} .\overrightarrow {{E_{21}}} \]
\[U = - {p_2}\dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\cos (\pi )\]
Angle between the dipole and electric field is 180 degrees.
\[U = \dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Now, to find the force
\[F = - \dfrac{{dU}}{{dx}} = \dfrac{3}{{4\pi {\varepsilon _ \circ }}}\dfrac{{{p_1}{p_2}}}{{{x^4}}}\]
F is positive, so it is a repulsive force.
Option (1) \[\dfrac{{3{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
Additional Information
Electric field due to dipole at a general point
\[E = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{p}{{{r^3}}}\sqrt {3{{\cos }^2}\theta + 1} \] , \[\theta \] =angle between the distance vector and dipole.
Potential due to dipole at a general point
\[V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _ \circ }{r^2}}}\]
Note
1. You need to keep in mind the direction of the electric field and dipole.
2. While using the formula of potential energy of dipole, you need to find the angle between field and dipole otherwise you will get the wrong force direction.
3. While finding electric fields, Approximation is made that the length of the dipole is negligible as compared to the distance of the point from the dipole.
Complete step-by-step Solution
A dipole is separation of two opposite charges and it is quantified by electric dipole moment and is denoted by p.
As we know electric field of dipole along perpendicular bisector of the axis,
\[\overrightarrow E = - \dfrac{{\overrightarrow p }}{{4\pi {\varepsilon _ \circ }{r^3}}}\] , where r= distance
\[{\varepsilon _ \circ }\] = permittivity of free space
\[{E_{21}}\] is the field due to dipole \[{p_1}\] at dipole \[{p_2}\]
\[{E_{21}} = \dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Potential energy of dipole system
\[U = - \overrightarrow {{p_2}} .\overrightarrow {{E_{21}}} \]
\[U = - {p_2}\dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\cos (\pi )\]
Angle between the dipole and electric field is 180 degrees.
\[U = \dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Now, to find the force
\[F = - \dfrac{{dU}}{{dx}} = \dfrac{3}{{4\pi {\varepsilon _ \circ }}}\dfrac{{{p_1}{p_2}}}{{{x^4}}}\]
F is positive, so it is a repulsive force.
Option (1) \[\dfrac{{3{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
Additional Information
Electric field due to dipole at a general point
\[E = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{p}{{{r^3}}}\sqrt {3{{\cos }^2}\theta + 1} \] , \[\theta \] =angle between the distance vector and dipole.
Potential due to dipole at a general point
\[V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _ \circ }{r^2}}}\]
Note
1. You need to keep in mind the direction of the electric field and dipole.
2. While using the formula of potential energy of dipole, you need to find the angle between field and dipole otherwise you will get the wrong force direction.
3. While finding electric fields, Approximation is made that the length of the dipole is negligible as compared to the distance of the point from the dipole.
Recently Updated Pages
A square frame of side 10 cm and a long straight wire class 12 physics JEE_Main

The work done in slowly moving an electron of charge class 12 physics JEE_Main

Two identical charged spheres suspended from a common class 12 physics JEE_Main

According to Bohrs theory the timeaveraged magnetic class 12 physics JEE_Main

ill in the blanks Pure tungsten has A Low resistivity class 12 physics JEE_Main

The value of the resistor RS needed in the DC voltage class 12 physics JEE_Main

Trending doubts
Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding Electromagnetic Waves and Their Importance

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Other Pages
Understanding Average and RMS Value in Electrical Circuits

Diffraction of Light - Young’s Single Slit Experiment

JEE Main 2025-26 Mock Test: Ultimate Practice Guide for Aspirants

Understanding Excess Pressure Inside a Liquid Drop

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Understanding Elastic Collisions in Two Dimensions




