Question

The force required just to move the body up an inclined plane is double the force required just to prevent the body from sliding down. If the coefficient of friction is $0.25$ the angle of inclination of the plane is
A. $36.8^\circ $
B. $45^\circ $
C. $30^\circ $
D. $42.6^\circ $

Answer 1

Hint: In order to solve this question we need to understand friction and Newton's second law of motion. Friction is an opposing force which always acts against the motion of the body and this force is directly proportional to normal on the body where coefficient of friction is proportionality constant. There are two types of friction one is static friction and other is kinetic friction, static friction acts on the body when the body is kept at rest while the kinetic friction acts on the body when the body is moving. So to move the body we just have to apply force which is equal or greater than friction.

Complete step by step answer:
Coefficient of friction is $\mu = 0.25$. Let the angle inclination of the plane be $\theta $. So while moving up the inclined plane, from the figure

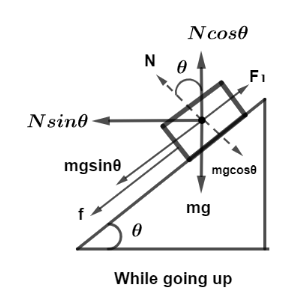
The normal is $N = mg\cos \theta $.
So the frictional force acts in downward direction along inclined plane is,
$f = \mu N$
$\Rightarrow f = \mu mg\cos \theta $
Also the component of gravity force in downward direction along inclined planes is $mg\sin \theta $. So total force that needed just to move up the inclined plane is given by,
$F = mg\sin \theta + f$
Putting values we get, $F = mg\sin \theta + \mu mg\cos \theta $

While moving down the inclined plane,

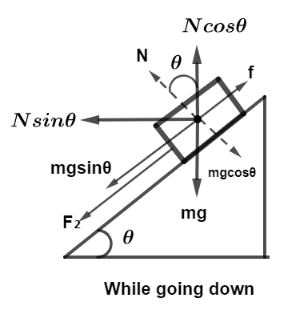
The normal is $N = mg\cos \theta $.
So the frictional force acts in upward direction along inclined plane is, $f = \mu N$
$f = \mu mg\cos \theta $
Also the component of gravity force in downward direction along inclined planes is $mg\sin \theta $.So total force that needed just to move up the inclined plane is given by,
${F_1} = mg\sin \theta - f$
Putting values we get,
${F_1} = mg\sin \theta - \mu mg\cos \theta $
So according to question,
$F = 2{F_1}$

Putting values we get,
$mg\sin \theta + \mu mg\cos \theta = 2(mg\sin \theta - \mu mg\cos \theta )$
$\Rightarrow 3\mu mg\cos \theta = mg\sin \theta $
$\Rightarrow 3\mu = \tan \theta $
$\Rightarrow \theta = {\tan ^{ - 1}}(3 \times 0.25)$
$\Rightarrow \theta = {\tan ^{ - 1}}(0.75)$
$\therefore \theta = 36.86^\circ $

So the correct option is A.

Note: It should be remembered that both the forces either frictional or downward component of gravitational force produce torque but in opposite direction and equal in magnitude so net torque is zero and that’s why body only translates rather than it rotates.There are four fundamental forces in nature.